Импульс тела. Импульс силы. Закон сохранения импульса. M 1 p
AM и PM при указании времени — это утро или вечер? Расшифровка и схема соответствия 24 и 12 часовых стандартов
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Вроде бы тривиальный вопрос, но насколько часто он возникает. Например, мне всегда трудно бывает сразу вспомнить при работе с англоязычными сервисами, а сколько это 10.00 PM в пересчете на наше время ощущение (это утро имеется в виду или вечер?). Да и вообще, откуда эти AM и PM взялись, кому они нужны и почему бы не пользоваться только исключительно 24-часовым форматом?


Ну, тут вопрос, наверное, из той же области, что и использование правостороннего движения автотранспорта в некоторых странах — так уж повелось и ничего тут уже не сделаешь. Нужно просто раз и навсегда разобраться с этими a.m. и p.m. (забить себе в голову взаимосвязь с 24-часовой линейкой), ну, или на худой конец написать себе шпаргалку (если как у меня в голове особо долго ничего не держится). А где написать? Да вот прямо тут, т.е. на страницах своего блога. Так и сделаю...
Так ли уж мы далеки от 12 часового формата времени?
Формат времени с использованием AM и PM распространен не только в буржунете, иногда его отголоски можно наблюдать на пространстве рунета (в основном у локализовавшихся буржуйских проектов). Например, известный многим блогерам сервис Фидбернер предлагает выбрать время рассылки писем подписчикам исходя именно из 12-часового формата, а не 24-часового:


Вроде и часовой пояс говорит о том, что тут a.m. и p.m. не понимают, и интерфейс переведен на русский язык. Ан нет, привычка — вторая натура. А мне как понимать 11:00 am — 1:00 pm? Это с одиннадцати утра до часу дня или же с одиннадцати вечера до часу ночи? Нужно гуглить, и так каждый раз, чтобы уж точно знать...
Хотя, я, наверное, зря так на буржуев накинулся с их AM и PM. Если вдуматься, то мы с вами тоже наполовину живем в 12-часовом мире. Например, вас когда время спрашивают, вы же не отвечаете, что сейчас без пятнадцати восемнадцать, а говорите, что без пятнадцати шесть, а вечера или утра — человек и сам определить в состоянии. В этом плане мы одинаковые.
В то же время в русскоязычных текстах в большинстве случаев (да всегда) используется 24-часовая шкала времени. Но вот часы стрелочные у нас опять же в 12-часовом формате. Наверное, 24 часа было бы сложно туда уместить и выглядело бы это перегруженным.


А вот цифровые часы у нас опять же 24-часовые, а у американцев они судя по фильмам, 12-часовые с указанием a.m. и p.m.


О, как все в жизни перепуталось, если задуматься.
Расшифровка и нюансы использования A.M. и P.M.
Но это все словоблудие, а что же означает это самое AM и PM (как эти аббревиатуры расшифровываются). Оказывается, что сокращения эти латинские и означают буквально следующее:
- AM — до полудня
- PM — после полудня (это, кстати, легче запомнить, ибо первые буквы в русском и латинском названии совпадают)
Это довольно хорошо можно проиллюстрировать такими вот двумя стрелочными хронометрами:


Если утрировать, то PM — это вечер, а AM — это утро. Вроде бы все просто, но есть маленькая проблема. Все хорошо, пока дело не доходит до полудня или полуночи, т.е. мест рандеву циклов a.m. и p.m.
В общем получается, что в разных странах, приемлющих 12-часовой цикл, эти моменты могут отмечать по-разному (и 12 p.m., и 12 a.m.). Таким образом, имеют место быть разночтения (типа, «стакан наполовину полон или он наполовину пуст»). По мне, так было бы логичнее использовать не 12 p.m., а 0 p.m., что было бы гораздо логичнее, но буржуям виднее. В итоге получается такая вот, на мой взгляд, нелепица:

После 12a.m. идет 01a.m. и т.д. А после 12p.m. идет 01p.m. Мне лично трудно привыкнуть (как может единица следовать после 12?). Американцы так вообще в документах полночь отмечают как 11:59 p.m., а полдень как 12:01 a.m., чтобы не возникало юридических казусов и разночтений. Странные они какие-то...
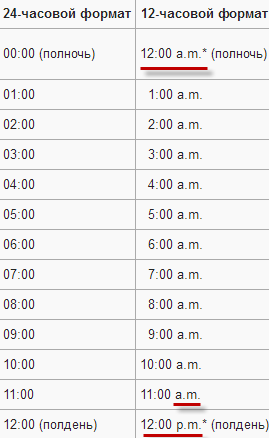
Таблица перевода из AM и PM в 24 часовой формат
Ну а полная табличка соответствия 12 и 24-часового формата времени будет выглядеть тогда так:
24-часовой формат12-часовой форматВ разговорной речи
| 00:00 (полночь) | 12:00 a.m. (полночь) | Двенадцать ночи |
| 01:00 | 1:00 a.m. | Час ночи |
| 02:00 | 2:00 a.m. | Два ночи |
| 03:00 | 3:00 a.m. | Три ночи |
| 04:00 | 4:00 a.m. | Четыре ночи |
| 05:00 | 5:00 a.m. | Пять утра |
| 06:00 | 6:00 a.m. | Шесть утра |
| 07:00 | 7:00 a.m. | Семь утра |
| 08:00 | 8:00 a.m. | Восемь утра |
| 09:00 | 9:00 a.m. | Девять утра |
| 10:00 | 10:00 a.m. | Десять утра |
| 11:00 | 11:00 a.m. | Одиннадцать утра |
| 12:00 (полдень) | 12:00 p.m. (полдень) | Двенадцать дня |
| 13:00 | 1:00 p.m. | Час дня |
| 14:00 | 2:00 p.m. | Два дня |
| 15:00 | 3:00 p.m. | Три дня |
| 16:00 | 4:00 p.m. | Четыре дня |
| 17:00 | 5:00 p.m. | Пять дня |
| 18:00 | 6:00 p.m. | Шесть вечера |
| 19:00 | 7:00 p.m. | Семь вечера |
| 20:00 | 8:00 p.m. | Восемь вечера |
| 21:00 | 9:00 p.m. | Девять вечера |
| 22:00 | 10:00 p.m. | Десять вечера |
| 23:00 | 11:00 p.m. | Одиннадцать вечера |
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Подборки по теме
Рубрика: Отвечаю на частые вопросы
ktonanovenkogo.ru
am vs pm, как не перепутать
Путешествовать легко! /
Полезное / Время a.m. и p.m - как не перепутать
12 am и 12 pm? Как запомнить раз и навсегда...
a.m. - до полудня, с 12 ночи до 12 дня, 1 a.m. - час ночи, 6 a.m. - 6 утра
p.m. - после полудня, с 12 дня до 12,
1 p.m. - час дня, 6 p.m. - 6 вечера
Если нас спрашивают, сколько времени, то мы обычно отвечаем: пол второго или
без пятнадцати три и т.п., не уточняя времени суток, ведь перепутать три дня и
три ночи довольно сложно. Другое дело, если речь идет о завтрашнем дне, о
назначаемой встрече или часах работы магазина. В этом случае мы используем
24-часовую систему - удобно и просто. Но во многих странах 24-часовая система
вовсе не распространена, и там используется 12-часовая система.
Как же американцы или европейцы узнают, о каком периоде суток идет речь? Они
используют аббревиатуры a.m. и p.m . Казалось бы, все просто: AM (от латинского ante meridiem) - это время до полудня,
то есть вроде как утро, а PM (post meridiem) - после полудня, вроде как вечер.
Но мне почему-то эти аббревиатуры никак не давались, я все время забывала, чего
там до полудня, а чего после, пока не поняла для себя важную вещь: день
всегда начинается с a.m .! Я имею в виду не свой день конечно (который часто и
после полудня начинается ))), а астрономический день, который всегда (!) начинается в
полночь (вспомните встречу Нового года).
То есть как и в 24-часовой системе,
первая секунда нового дня в формате a.m./p.m. выглядит так 00.00.01 a.m.
, а собственно полночь - 12.00 a.m.
Однако чтобы избежать конфуза в случае 12 ночи и 12 дня рекомендуется уточнять время таких
образом: для полночи использовать 12 midnight, а для полудня 12
noon.
Совет от Димы: (мнемонические правила) буква а - аврора - богиня утренней зари, буква р (русское п, читаешь же как пи-эм) - от слова "Позднее время", или Поздно
|
tago.narod.ru
Основные формулы теории вероятности / Теория вероятности / 3dstroyproekt.ru
| №№ п/п | Понятия, обозначения | Содержание, формула |
| 1 | Множество | Множество $A-$ совокупность каких-либо объектов $a$, называемых элементами множества: $a\in A$ |
| 2 | Дополнение $\overline A $ { не $A$ } | $\overline A $ содержит все элементы, не принадлежащие $A$ |
| 3 | Равенство множеств $A=B$ | Два множества $A$ и $B$ равны между собой, если они состоят из одних и тех же элементов |
| 4 | Объединение { сумма } множеств $C=A+B$ | Множество $C$ состоит из всех элементов, принадлежащих или множеству $A$, или множеству $B$ или и $A$ и $B$ одновременно |
| 5 | Пересечение { произведение } множеств $C=A\cdot B$ | Множество $C$ состоит из элементов, принадлежащих одновременно и множеству $A$ и множеству $B$ |
| 6 | Разность двух множеств $C=A-B$ | $C$ состоит из элементов множества $A$, которые не являются элементами множества $B$ |
| 7 | Эквивалентные множества | Два множества называются эквивалентными, если между ними установлено взаимно-однозначное соответствие. |
| 8 | Счетные множества | Бесконечные множества, эквивалентные множеству натуральных чисел $\mathbb { N } $ |
| 9 | Перестановки. Число перестановок | Соединения, отличающиеся только порядком элементов, называются перестановками. Число перестановок из $n$ элементов $P_n =n!$, где $n!=1\cdot 2\cdot 3\cdot 4\cdot \ldots \cdot n$ $0!=1$ |
| 10 | Размещения. Число размещений | Соединения из $n$ различных элементов по $m$, отличающихся друг от друга составом элементов либо их порядком, называются размещениями. Число размещений из $n$ по $m$ $A_n^m =\frac { n! } { (n-m)! } $ |
| 11 | Сочетания. Число сочетаний | Соединения из $n$ различных элементов по $m$, отличающихся друг от друга хотя бы одним элементом, называются сочетаниями. Число сочетаний из $n$ по $m$ $C_n^m =\frac { n! } { (n-m)!m! } $ $C_n^m =C_n^ { n-m } ;$ $C_n^0 =1; C_ { n+1 } ^ { m+1 } =C_n^m +C_n^ { m+1 } ;$ $C_n^0 +C_n^1 +C_n^2 +\ldots +C_n^ { n-1 } +C_n^n =2^n$ |
| 12 | Стохастический эксперимент | Это опыт { испытание } , результат которого заранее не определен |
| 13 | Достоверное событие | Результат, который обязательно наступает при осуществлении данного комплекса условий { опыта, эксперимента } называется достоверным событием |
| 14 | Случайное событие | Это событие, которое может произойти, а может и не произойти в данном испытании |
| 15 | Невозможное событие | Это событие, которое не может произойти при данном комплексе условий |
| 16 | Относительная частота события $A$ | Отношение $\nu (A)=\frac { m } { n } $ числа экспериментов $m$, завершившихся событием $A$, к общему числу $n$ проведенных экспериментов |
| 17 | Статистическое определение вероятности | Если при неограниченном увеличении числа экспериментов относительная частота события $\nu (A)$ стремится к некоторому фиксированному числу, то событие $A$ стохастически устойчиво и это число $p(A)$ называют вероятностью события $A$ |
| 18 | Определение вероятности в классической схеме | $P(A)=\frac { m } { n } $, где $m$ – число исходов стохастического эксперимента, благоприятствующих наступлению события $A$, $n$ – общее число всех равновозможных исходов |
| 19 | Вероятность суммы { объединения } , двух событий $A$ и $B$ | $P(A+B)=P(A)+P(B)-P(AB)$ |
| 20 | Вероятность произведения двух зависимых событий $A$ и $B$ | $P(AB)=P(A)\cdot P(B/A)=P(B)\cdot P(A\vert B)$, где $P(B\vert A)$ – условная вероятность события $B$ при условии, что событие $A$ с ненулевой вероятностью произошло |
| 21 | Независимые события $A$ и $B$ | Это такие события, для которых $P(B\vert A)=P(B)$ и $P(A\vert B)=P(A)$. Следовательно, $P(AB)=P(A)\cdot P(B)$ |
| 22 | Схема Бернулли | Стохастический эксперимент состоит из последовательности $n$ независимых и одинаковых испытаний, в каждом из которых может произойти событие $A$ или событие, ему противоположное $\overline A $ с вероятностями соответственно равными $p$ и $q=1-p$ |
| 23 | Формула Бернулли | Вероятность того, что в серии из $n$ испытаний событие $A$ появится ровно $m$ раз $P_n (m)=C_n^m \cdot p^m\cdot q^ { n-m } $ |
| Вероятность того, что при $n$ испытаниях $A$ появляется не менее $m_1 $ и не более $m_2 $ раз вычисляется по формуле: $P_n (m_1 \leqslant m\leqslant m_2 )=\sum\limits_ { m=m_1 } ^ { m_2 } { C_n^m \cdot p^m\cdot q^ { n-m } } $ |
| 24 | Формула Пуассона | При достаточно большом $n$ и малом $p$, если $a=np\lt 10\rightarrow P_n (m)\approx \frac { a^m } { m! } e^ { -a } $ { таблица 1 } |
| $P_n (m\leqslant k)\approx e^ { -a } \sum\limits_ { m=0 } ^k { \frac { a^m } { m! } } $ { таблица 2) |
| 25 | Локальная формула Муавра-Лапласа | При достаточно большом $n$ и не слишком малых $p$ и $q$ $P_n (m)\approx \frac { 1 } { \sqrt { npq } } \phi (x)$, где $\varphi (x)=\frac { 1 } { \sqrt { 2\pi } } e^ { \frac { -x^2 } { 2 } } $ и $x=\frac { m-np } { \sqrt { npq } } $; $\phi (-x)=\phi (x)$ { таблица 3) |
| 26 | Интегральная формула Муавра – Лапласа | $P_n (m_1 \leqslant m\leqslant m_2 )=\Phi (x_2 )-\Phi (x_1 )$, где $x_1 =\frac { m_1 -np } { \sqrt { npq } } $; $x_2 =\frac { m_2 -np } { \sqrt { npq } } $; $\Phi (x)=\frac { 1 } { \sqrt { 2\pi } } \int\limits_0^x { e^ { \frac { -t^2 } { 2 } } } dt$; $\Phi (-x)=-\Phi (x)$ { таблица 4 } |
| 27 | Понятие случайной величины | Случайной величиной называют переменную величину, которая принимает числовые значения в зависимости от исходов испытания случайным образом. |
| 28 | Понятие дискретной случайной величины { ДСВ $X$ } | ДСВ $X$ – случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, то есть численные значения которой образуют конечное или счетное множество. |
| 29 | Закон распределения дискретной случайной величины | Соответствие между значениями $x_1, x_2, \cdots $ дискретной случайной величины и их вероятностями $p_1, p_2, \cdots $ называется законом распределения и может быть задан таблично или аналитически { то есть с помощью формул } . Если ДСВ $X$ принимает конечное множество значений $x_1 ,x_2 ,x_3 ...$ соответственно с вероятностями $p_1 ,p_2 ,...,p_n $, то ее закон распределения определяется формулами $P(X=x_k )=p_k , ~k=1,2,...,n$ и $\sum\limits_ { k=1 } ^n { p_k =1 } $ Если ДСВ $X$ принимает бесконечную последовательность значений $x_1 ,x_2 ,x_3 ...$ соответственно с вероятностями $p_1 ,p_2 ,p_3 ,...$, то ее закон распределения определяется формулами $P(X=x_k )=p_k, ~k=1,2,...,n$ и $\sum\limits_ { k=1 } ^\infty { p_k =1 } $ |
| 30 | Понятие непрерывной случайной величины { НСВ $X$ } | НСВ $X$ – случайная величина, которая может принимать любые значения из некоторого промежутка, то есть множество значений непрерывной случайной величины несчетно. |
| 31 | Функция распределения. Свойства функции распределения | Функцией распределения случайной величины $X$ называется функция действительного переменного $x$, определяемая равенством $F(x)=P(X\lt x)$, где $P(X\lt x)$ - вероятность того, что случайная величина $X$ принимает значение, меньше $x$ Функция распределения $F(x)$ для ДСВ $X$, которая может принимать значения $x_1 ,x_2 ,...x_n $ c соответствующими вероятностями $p_1 ,p_2 ,...,p_n$ имеет вид $F(x)=\sum\limits_ { x_k \lt x } { P(X\lt x_k ) } $, где символ $x_k \lt x$ означает, что суммируются вероятности $p_k $ тех значений, которые меньше $x$. Функция является разрывной. Случайная величина $X$ называется непрерывной, если ее функция распределения $F(x)$ является непрерывно дифференцируемой. Вероятность того, что СВХ примет значение из промежутка $\left[ { \alpha ;\beta }\right)$, равна разности значений ее функции распределения на концах этого полуинтервала: $P(\alpha \leqslant X\lt \beta )=F(\beta )-F(\alpha )$ Свойства функции распределения 1. $0\leqslant F(x)\leqslant 1$ 2. Если $x_1 \lt x_2 $, то $F(x_1 )\leqslant F(x_2 )$, то есть функция распределения является неубывающей. |
| 31 | Функция распределения. Свойства функции распределения | 3. Функция $F(x)$ в точке $x_0 $ непрерывна слева, то есть $\mathop { \lim } \limits_ { x\to x_0 -0 } F(x)=F(x_0 )$; $F(x_0 -0)=F(x_0 )$ 4. Если все возможные значения СВХ принадлежат интервалу $(a;b)$, то $F(x)=0$ при $x\leqslant a$, $F(x)=1$ при $x\geqslant b$ 5. Если все возможные значения СВХ принадлежат бесконечному интервалу $\left( { -\infty ;+\infty }\right)$, то $\mathop { \lim } \limits_ { x\to -\infty } F(x)=0;\mathop { \lim } \limits_ { x\to +\infty } F(x)=1;$ Если $X$ – непрерывная случайная величина, то вероятность того, что она примет одно заданное определенное значение, равна нулю: $P(X=\alpha )=0$ Отсюда следует, что для непрерывной случайной величины выполняются равенства: $P(\alpha \lt X\lt \beta )=P(\alpha \leqslant X\leqslant \beta )=P(\alpha \leqslant X\lt \beta )=$ $=P(\alpha \lt X\leqslant \beta )=F(\beta )-F(\alpha )$ |
| 32 | Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения. | Плотностью распределения { дифференциальной функцией распределения } вероятностей НСВ $X$ в точке $x$ называют предел отношения вероятности попадания значений этой величины в интервал $\left( { x;x+\Delta x }\right)$ к длине $\Delta x$ этого интервала, когда последняя стремится к нулю: $f(x)=\mathop { \lim } \limits_ { \Delta x\to 0 } \frac { P(x\lt X\lt x+\Delta x) } { \Delta x } $ Следовательно, $f(x)= { F } '(x)$, то есть плотность распределения есть первая производная от функции распределения НСВХ. Вероятность того, что НСВХ примет значение, принадлежащее интервалу $(a;b)$, определяется равенством $P(a\lt X\lt b)=\int\limits_a^b { f(x)dx } $ |
| 32 | Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения. | Зная плотность распределения, можно найти функцию распределения $F(x)=\int\limits_ { -\infty } ^x { f(x)dx } $ Свойства функции плотности 1. Плотность распределения $f(x)$ - неотрицательная функция, то есть $f(x)\geqslant 0$ 2. Несобственный интеграл по бесконечному промежутку $\left( { -\infty ;+\infty }\right)$ от функции плотности вероятностей равен единице: $\int\limits_ { -\infty } ^ { +\infty } { f(x)dx=1 } $ 3. Если все возможные значения случайной величины принадлежат отрезку $\left[ { \alpha ;\beta }\right]$, то $\int\limits_\alpha ^\beta { f(x)dx=1 } $, так как вне этого промежутка $f(x)=0$ |
| 33 | Математическое ожидание | Для ДСВ $X$ равно сумме произведений всех ее значений на соответствующие вероятности: $M(X)=\sum\limits_ { i=1 } ^n { x_i p_i } $ Для НСВ $X:\;M(X)=\int\limits_ { -\infty } ^ { +\infty } { xf(x)dx } $, где $f(x)=F'(x)$ – функция плотности распределения вероятности. |
| 34 | Свойства математического ожидания | 1. $M(C)=C$, если $C=const,$ 2. $M(CX)=CM(X),$ 3. $M(X+Y)=M(X)+M(Y),$ 4. Если $X$ и $Y$ – независимые случайные величины, то $M(XY)=M(X)\cdot M(Y)$ |
| 35 | Дисперсия случайной величины | Разность $X-M(X)$ называется отклонением случайной величины $X$ от ее математического ожидания $M(X)=a$. Математическое ожидание отклонения равно нулю: $M(X-a)=0$ Дисперсией, или рассеянием случайной величины $X$ называется математическое ожидание квадрата ее отклонения: $D(X)=M((X-a)^2)$ Следовательно, для любой случайной величины $X:\;\;D(X)\geqslant 0$ |
| 36 | Свойства дисперсии | 1. $D(C)=0$, $C=const,$ 2. $D(CX)=C^2D(X)$, $C=const,$ 3. Если случайные величины $X$ и $Y$ независимы, то $D(X\pm Y)=D(X)+D(Y),$ 4. $D(XY)=D(X)\cdot D(Y),$ 5. $D(X)=M(X^2)-(M(X))^2.$ |
| 37 | Среднее квадратическое отклонение | Среднеквадратическим отклонением, или стандартным отклонением, случайной величины $X$ называется корень квадратный из ее дисперсии: $\sigma (X)=\sqrt { D(X) } \Leftrightarrow D(X)=\sigma ^2.$ |
| 38 | Биномиальное распределение | Закон распределения дискретной случайной величины, определяемой формулой Бернулли $p_k =P_n (k)=C_n^k \cdot p^k\cdot q^ { n-k } (k=0,1,2,...,n)$ называется биномиальным. Постоянные $n,~p$ называются параметрами биномиального распределения $\left( { q=1-p }\right)$. $M(X)=np;\;D(X)=npq;\;\sigma (X)=\sqrt { npq } $ |
| 39 | Распределение Пуассона | Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой Пуассона $P_n (k)=\frac { a^ke^ { -a } } { k! } $, где $a=np$ – параметр распределения. $M(X)=a;D(X)=a$ |
| 40 | Равномерное распределение на интервале $\left( { a;b }\right)$ | Если значения случайной величины, которые она принимает в конечном промежутке $(a;b)$, возможны в одинаковой степени, то плотность распределения вероятностей этой величины постоянна на данном промежутке и равна нулю вне этого промежутка, то есть $f(x)=\left\{ { \begin{array} { l } C\;\mbox { на } \;\left[ { a,b }\right], \\ 0\;\mbox { вне } \;(a,b). \\ \end{array} }\right.$ Доказано, что $C=\frac { 1 } { b-a } .$ $M(X)=\frac { a+b } { 2 } ; ~ D(X)=\frac { (b-a)^2 } { 12 } ; ~ \sigma (X)=\frac { b-a } { 2\sqrt 3 } $ |
| 41 | Геометрическое распределение | Геометрическим называется распределение дискретной случайной величины $X$, определяемое формулой $P(X=m)=(1-p)^ { m-1 } \cdot p,$, где $0\lt p\lt 1$, и $m=1,2,3...$ { Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем $q=1-p$ } . $M(X)=\frac { 1 } { p } ; ~ D(X)=\frac { 1-p } { p^2 } $ |
| 42 | Показательное распределение | Показательным называется распределение с плотностью вероятностей, определяемой по формуле $f(x)=\left\{ { \begin{array} { l } 0\mbox { при } \;x\lt 0, \\ \lambda e^ { -\lambda x } \mbox { } \;\mbox { при } \;x\geqslant 0, \\ \end{array} }\right.$ где $\lambda >0$ - параметр распределения. $M(X)=\frac { 1 } { \lambda } ; ~ D(X)=\frac { 1 } { \lambda ^2 } \quad ; ~ \sigma (X)=\frac { 1 } { \lambda } .$ Замечание. Если $T$ – время безотказной работы элемента, $\lambda $ - интенсивность отказов, то случайная величина $T$ распределена по экспоненциальному закону с функцией распределения $F(t)=P(T\lt t)=1-e^ { -\lambda t } ,_ { } $ где $\lambda \gt 0$. $F(t)$ определяет вероятность отказа элемента за время $t$. Вероятность безотказной работы элемента за время $t$ равна $e^ { -\lambda t } $. Функция $R(t)=e^ { -\lambda t } $ называется функцией надежности. |
| 43 | Нормальное распределение $N(a;\sigma )$ | Нормальным распределением, или распределением Гаусса, называется распределение с плотностью вероятностей $f(x)=\frac { 1 } { \sigma \sqrt { 2\pi } } e^ { \frac { -(x-a)^2 } { 2\sigma ^2 } } $ Постоянные $a$ и $\sigma \quad (\sigma \gt 0)$ называются параметрами нормального распределения. $M(X)=a; ~ D(X)=\sigma ^2; ~ \sigma =\sqrt { D(X) } $ Вероятность попадания значений нормальной случайной величины $X$ в интервале $(\alpha ;\beta )$ определяется формулой $P(\alpha \lt X\lt \beta )=\Phi (\frac { \beta -\alpha } { \sigma } )-\Phi (\frac { \alpha -a } { \sigma } ),$ где $\Phi (x)$ – функция Лапласа. $M(X)=a; D(X)=\sigma ^2.$ |
| 44 | Нормированное распределение $N(0;1)$ | Нормированным или стандартным называется такое нормальное распределение непрерывной случайной величины, когда функция плотности вероятностей $f(x)=\frac { 1 } { \sqrt { 2\pi } } e^ { \frac { -x^2 } { 2 } } .$ $M(X)=a=0; ~ \sigma (X)=\sigma =1.$ |
| 45 | Мода случайной величины $\overline M $ | Модой ДСВ $X$ называется ее наиболее вероятное значение. Модой НСВ $X$ называется то ее значение, при котором плотность распределения вероятностей максимальна. |
| 46 | Медиана $M_e $ | Медианой непрерывной случайной величины $X$ называется такое ее значение $M_e $, для которого одинаково вероятно, окажется ли случайная величина меньше или больше $M_e $, то есть $P(x\lt M_e )=P(x>M_e )=0,5$. Если прямая $x=a$ является осью симметрии кривой распределения $f(x)$, то $\overline M =M_e =M(X)=a$. |
| 47 | Начальные моменты $\nu _k $ | Начальным моментом $\nu _k ~ k$ -го порядка случайной величины $X$ называется математическое ожидание $k$-ой степени этой случайной величины: $\nu _k =M(X^k)$. Для ДСВ $X:_ { } \nu _k =\sum\limits_ { i=1 } ^n { x_i^k \cdot p_i } $, где $\sum\limits_ { i=1 } ^\infty { p_i =1 } $. Начальный момент $k$-го порядка НСВ $X$ с плотностью распределения $f(x)$ определяется формулой : $\nu _k =\int\limits_ { -\infty } ^ { +\infty } { x^kf(x)dx } $, где $\int\limits_ { -\infty } ^ { +\infty } { f(x)dx=1 } $. |
| 48 | Центральные моменты $\mu _k $ | Центральным моментом $\mu _k ~ k$-го порядка случайной величины $X$ называется математическое ожидание $k$-ой степени отклонения этой величины от ее математического ожидания. Если обозначить $M(X)=a$, то $\mu _k =M((X-a)^k)$ Для ДСВ $X: \quad \mu _k =\sum\limits_ { i=1 } ^n { (x_i -a)^k\cdot p_i } $, если множество этой величины конечно, а если – счетно, то $\mu _k =\sum\limits_ { i=1 } ^\infty { (x_i -a)^k\cdot p_i } .$ Для НСВ $X$ с плотностью распределения $f(x)$ центральный момент $k$-го порядка определяется формулой: $\mu _k =\int\limits_ { -\infty } ^ { +\infty } { (x_i -a)^k\cdot f(x)dx } .$ |
| 49 | Некоторые свойства начальных и центральных моментов | $\nu _0 =1;~ \nu _1 =M(X),$ $\mu _0 =1;~ \mu _1 =0;~ ~ \mu _2 =D\left( X \right),$ $\mu _2 =\nu _2 -\nu _1^2 ,$ $\mu _3 =\nu _3 -3\nu _1 \nu _2 +2\nu _1^3 ,$ $\mu _4 =\nu _4 -4\nu _1 \nu _3 +6\nu _1^2 \nu _2 -3\nu _1^4 .$ |
| 50 | Асимметрия | Отношение центрального момента 3-го порядка к кубу среднеквадратического отклонения случайной величины называется асимметрией: $A(X)=\frac { \mu _3 } { \sigma ^3 } $. Если распределение случайной величины симметрично относительно ее математического ожидания, то асимметрия равна нулю. |
| 51 | Эксцесс | Эксцессом случайной величины называется величина $Э_x =\frac { \mu _4 } { \sigma ^4 } -3.$ Для нормального распределения $Э_x =0$. Кривые, более островершинные по сравнению с нормальной кривой Гаусса, имеют $Э_x \gt 0$. У более плосковершинных кривых $Э_x \lt 0.$ |
3dstroyproekt.ru
Импульс тела. Импульс силы. Закон сохранения импульса | LAMPA
Закон сохранения импульса
Импульс вводился не случайно. Оказывается, импульс тела никуда не девается — он сохраняется. Мы предлагаем вам убедиться в этом. Рассмотрим простой случай — столкновение двух шаров.
То, что будет происходить между этими двумя шарами, можно изобразить на рисунке. При этом можно выделить три этапа:
- ситуация "до" (до столкновения)
- само столкновение
- ситуация "после" (после столкновения).
 "До": шары летели навстречу друг к другу; "после": шары разлетелись после столкновения; столкновение: шары действовали друг на друга.
"До": шары летели навстречу друг к другу; "после": шары разлетелись после столкновения; столкновение: шары действовали друг на друга.
Нам интересен момент столкновения. Первый шар действует на второй с силой F⃗21\vec{F}_{21}F⃗21, а второй шар действует на первый с силой F⃗12\vec{F}_{12}F⃗12. По 3-му закону Ньютона эти силы равны друг другу по модулю и противоположны по направлению:
F⃗21=−F⃗12\vec{F}_{21}=-\vec{F}_{12}F⃗21=−F⃗12.
Домножим это равенство на длительность столкновения Δt\Delta tΔt:
F⃗21⋅Δt=−F⃗12⋅Δt\vec{F}_{21}\cdot\Delta t=-\vec{F}_{12}\cdot\Delta tF⃗21⋅Δt=−F⃗12⋅Δt.
У нас получились импульсы сил, действующие на каждое из тел. Мы помним, импульс силы равен изменению импульса тела. Можем записать:
Δp⃗2=−Δp⃗1\Delta\vec{p}_2=-\Delta\vec{p}_1Δp⃗2=−Δp⃗1.
Распишем изменение импульсов тел. Буквой VVV будем обозначать скорости до столкновения, а буквой UUU — скорости после столкновения.
m2(U⃗2−V⃗2)=−m1(U⃗1−V⃗1)m_2(\vec{U}_2-\vec{V}_2)=-m_1(\vec{U}_1-\vec{V}_1)m2(U⃗2−V⃗2)=−m1(U⃗1−V⃗1).
Если отбросить знак "минус", то изменения импульсов тел равны друг другу. Можно заметить интересную вещь: если два тела разной массы сталкиваются, то скорость более легкого тела (с меньшей массой) в результате столкновения изменится сильнее.
Продолжаем наши преобразования:
m2U⃗2−m2V⃗2=−(m1U⃗1−m1V⃗1)m_2\vec{U}_2-m_2\vec{V}_2=-(m_1\vec{U}_1-m_1\vec{V}_1)m2U⃗2−m2V⃗2=−(m1U⃗1−m1V⃗1),
m2U⃗2−m2V⃗2=−m1U⃗1+m1V⃗1m_2\vec{U}_2-m_2\vec{V}_2=-m_1\vec{U}_1+m_1\vec{V}_1m2U⃗2−m2V⃗2=−m1U⃗1+m1V⃗1,
m2U⃗2+m1U⃗1=m2V⃗2+m1V⃗1m_2\vec{U}_2+m_1\vec{U}_1=m_2\vec{V}_2+m_1\vec{V}_1m2U⃗2+m1U⃗1=m2V⃗2+m1V⃗1.
Что получилось? Получился закон сохранения импульса.
Закон сохранения импульса. Векторная сумма импульсов тел до взаимодействия равна векторной сумме импульсов тел после взаимодействия:векторная сумма того, что было "до" = векторная сумма того, что стало "после".
Небольшое дополнение. Мы рассматривали ситуацию, в которой не было никаких внешних сил: никто "извне" не действовал на шары. Закон сохранения импульса справедлив для случая, когда внешние силы не действуют на систему тел или же действие внешних сил скомпенсировано. Такие системы тел называются замкнутыми.
Порешаем задачки.
Условие
Одинаковые шары движутся с одинаковыми по модулю скоростями в направлениях, указанных стрелками на рисунке, и абсолютно неупруго соударяются.

Как будет направлен импульс шаров после их столкновения?
- ↙\swarrow↙
- ←\leftarrow←
- ↓\downarrow↓
- ↖\nwarrow↖
(Источник: ЕГЭ-2014. Физика. Досрочный этап. Вариант 1)
Решение
Начнем с того, что поясним, что такое "неупругий удар". Неупругий удар или столкновение — это столкновение, которое приводит к "слипанию" соударяющихся тел. При неупругом ударе не выполняется закон сохранения механической энергии. Но об этом в следующих темах. В этой задаче для нас важно то, что после соударения тела будут двигаться вместе — "слипнутся".
В задаче говорится о том, что было "до", а спрашивается про то, что стало "после". Даны направления скоростей. Очень похоже на то, что это задача на закон сохранения импульса. Что мы знаем из него? Мы знаем, что в замкнутой системе тел векторная сумма импульсов тел "до" соударения равна векторной сумме импульсов тел "после":
m1U⃗1+m2U⃗2=m1V⃗1+m2V⃗2m_1\vec{U}_1+m_2\vec{U}_2=m_1\vec{V}_1+m_2\vec{V}_2m1U⃗1+m2U⃗2=m1V⃗1+m2V⃗2.
В нашем случае m1=m2=mm_1=m_2=mm1=m2=m, а после столкновения шары "слипаются", поэтому закон сохранения импульса примет вид
mU⃗1+mU⃗2=2mV⃗m\vec{U}_1+m\vec{U}_2=2m\vec{V}mU⃗1+mU⃗2=2mV⃗,
где V⃗\vec{V}V⃗ — скорость совместного движения шаров после столкновения, а U⃗1\vec{U}_1U⃗1 и U⃗2\vec{U}_2U⃗2 — скорости шаров до столкновения. Направление импульса шаров после столкновения, о котором спрашивается в задаче, — это направление вектора 2mV⃗2m\vec{V}2mV⃗.
Как его найти? Направление вектора в правой части равенства совпадает с направлением вектора в левой части равенства. Попробуем сложить импульсы шаров до столкновения, чтобы получить векторную сумму импульсов и определить ее направление.
Направления импульсов до столкновения нам известны (направления импульсов совпадают с направлениями скоростей, а они указаны на рисунке). Так как шары были одинаковыми и двигались с одинаковыми скоростями, модули импульсов шаров были равны. Складываем векторы импульсов по правилу параллелограмма.
 Видно, что суммарный импульс направлен влево. По закону сохранения импульса в ситуации "после" суммарный импульс будет направлен точно так же. Значит, подходит ответ 2).
Видно, что суммарный импульс направлен влево. По закону сохранения импульса в ситуации "после" суммарный импульс будет направлен точно так же. Значит, подходит ответ 2).
Ответ. 2) ←\leftarrow←
Решим еще одну задачу.
Условие
Мальчик массой 505050 кг находится на тележке массой 505050 кг, движущейся по гладкой горизонтальной дороге со скоростью 111 м/с. Каким станет модуль скорости тележки, если мальчик прыгнет с нее со скоростью 222 м/с относительно дороги в направлении, противоположном первоначальному направлению движения тележки? Ответ выразите в м/с.
(Источник: ЕГЭ-2013. Физика. Реальный экзамен)
Решение
Шаг 1. Мы думаем, что вы согласитесь с тем, что без рисунка непросто представить, что именно происходит в этой задаче. Давайте сделаем рисунок. У нас на рисунке будут изображены две ситуации: ситуация "до" и ситуация "после". На рисунке кроме самих предметов нужно также указать направление скоростей и ось, на которую мы будем проецировать эти скорости. Должно получиться что-то вроде этого:
 Шаг 2. Отлично! Теперь можно записать закон сохранения импульса в векторной форме.
Шаг 2. Отлично! Теперь можно записать закон сохранения импульса в векторной форме.
lampa.io









 "До": шары летели навстречу друг к другу; "после": шары разлетелись после столкновения; столкновение: шары действовали друг на друга.
"До": шары летели навстречу друг к другу; "после": шары разлетелись после столкновения; столкновение: шары действовали друг на друга.
 Видно, что суммарный импульс направлен влево. По закону сохранения импульса в ситуации "после" суммарный импульс будет направлен точно так же. Значит, подходит ответ 2).
Видно, что суммарный импульс направлен влево. По закону сохранения импульса в ситуации "после" суммарный импульс будет направлен точно так же. Значит, подходит ответ 2). Шаг 2. Отлично! Теперь можно записать закон сохранения импульса в векторной форме.
Шаг 2. Отлично! Теперь можно записать закон сохранения импульса в векторной форме.






