до какой скорости мальчик разгонит стоящие на снегу санки , прикладываю силу 10Н в течение 0.5с? Масса санок 2.5кг. , действием силы трения пренебречь
U2/U1=I1/I2
I2=U1*I1/U2=5*0,5/20=0,125 А
a = V / t = 5 / 10 = 0,5 м/с²
Потому что сила натяжения направлена в противоположную сторону.
Осеней подготовка земли к посеву растений весенней удобрение земли и что бы она дышала
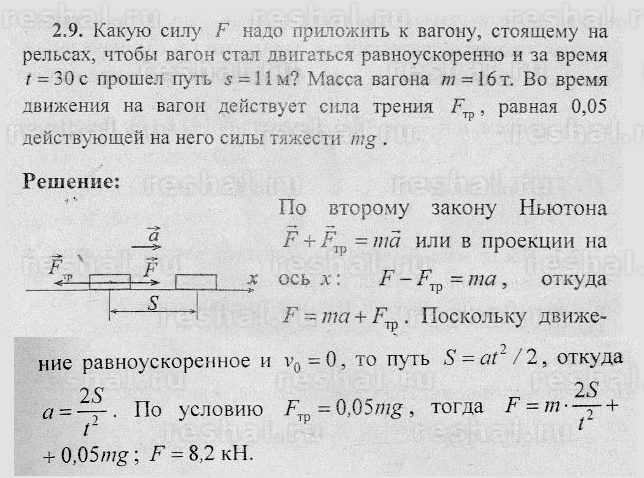 Амперметр присоединяется последовательно к тому участку цепи, на котором надо измерить силу тока, при этом соблюдая полярность (+ амперметра к + источника, — амперметра к — источника).
Амперметр присоединяется последовательно к тому участку цепи, на котором надо измерить силу тока, при этом соблюдая полярность (+ амперметра к + источника, — амперметра к — источника).Почему амперметр подключается последовательно?
Вспомним, что при последовательном соединении сила тока на амперметре будет равна силе тока на том участке цепи, где её следует измерить. Т.е. амперметр будет на самом деле измерять силу тока «на себе», а результат будет справедлив для того участка цепи, на котором нужно было измерить силу тока.
2. Вольтметр подключается паралельно к тому участку цепи, на котором нужно измерить напряжение, так же соблюдая полярность.
Почему вольтметр следует подключать параллельно?
Вспомним, что при параллельном соединении напряжение на вольтметре будет равно напряжению на том участке цепи, где его следует измерить. Поэтому вольтметр, измеряя напряжение «на себе», одновременно будет получать результат для того участка цепи.
3. Напряжение равно произведению силы тока на сопротивление цепи по закону Ома
Задание по физике в 10 кл.
 при дистанционном обучении по теме «Закон сохранения импульса».
при дистанционном обучении по теме «Закон сохранения импульса».Образец задания по физике в 10 классе при дистанционном обучении (асинхронное обучение на вечернем отделении).
Урок по физике 10 класс 12.11. 2020г.
Учитель Соколова Т.И.
Тема урока «Закон сохранения импульса».
Задание ученику:
1.Ознакомиться с конспектом по теме (конспект прилагается)
2.Выполнить тезисный конспект (краткий).
3. Ответить на вопросы.
4. Решить задачи.
Образец выполнения работы
Физика 10 класс Ф.И. 12.11.2020
Ответ напечатать на отдельном листе и переслать мне на почту.
1. Конспект.
1. Изменение импульса тела или системы тел равно сумме импульсов сил, действующих на это тело или систему тел.
Записав в этом выражении импульсы в виде
произведений массы на соответствующие скорости, произведём математические
преобразования. Получим
Получим
Однако по определению а значит, проделав математические преобразования, можно перейти к записи второго закона Ньютона:
Вспомним, что приведённое определение ускорения в общем случае справедливо только при рассмотрении малого изменения скорости за малый промежуток времени. А верна ли формула (1), если промежуток времени малым считать нельзя? Поскольку любой промежуток времени можно разбить на множество малых интервалов и затем произвести суммирование изменений импульса за каждый из этих интервалов времени, то формула (1) оказывается верной независимо от значения промежутка времени.
Проиллюстрировать это можно с помощью уже известного
вам опыта с гирей и двумя нитями (см. рис. 20, а). Если дергать за нижнюю нить
резко, то время действия силы будет малым и импульса силы будет не достаточно
для существенного изменения импульса гири (см. рис. 20, б). Если же за нижнюю
нить тянуть медленно, то время действия силы увеличивается, а значит,
увеличивается и её импульс. В этом случае импульс силы может существенно
изменить импульс гири (см. рис. 20, в).
В этом случае импульс силы может существенно
изменить импульс гири (см. рис. 20, в).
Проведём опыт. На стакан положим картонную пластинку, а сверху монету (рис. 39, а). Если картонку медленно сдвигать, то монета будет сдвигаться вместе с ней. Но если резким ударом выбить картонку, то монета упадёт в стакан (рис. 39, б). Объяснить этот опыт также можно, применяя теорему об изменении импульса. Когда картонка движется медленно, время действия силы трения на монету достаточно для изменения её импульса, и монета приходит в движение вместе с картонкой. Если же картонка резко выбивается, то время действия силы трения оказывается крайне малым, и импульса силы недостаточно для того, чтобы сдвинуть монету: она остаётся на месте. Но после того как картонка выбита, лишённая опоры монета падает в стакан.
2. Напомним, что при взаимодействии двух тел изменение импульса первого тела равно импульсу силы, действующей на него со стороны второго тела:
откуда
Далее необходимо получить
формулу закона сохранения импульса, разобравшись с математическими выкладками
на стр. 63 учебника.
63 учебника.
Импульс каждого из взаимодействующих тел изменился, однако векторная сумма их импульсов осталась неизменной.
Рассмотренная система состояла из двух тел. Однако полученные выводы справедливы и в общем случае, когда система состоит из любого числа тел и является замкнутой: тела, составляющие такую систему, взаимодействуют между собой и не взаимодействуют с другими телами.
Равенство (2) называют законом сохранения импульса.
Векторная сумма импульсов тел, составляющих замкнутую систему, остаётся постоянной при любых взаимодействиях этих тел между собой. |
Проиллюстрировать закон
сохранения импульса можно с помощью установки, состоящей из нескольких
одинаковых шаров, подвешенных таким образом, что их центры лежат на одной
прямой (рис. 40, а). Если отвести в сторону крайний левый шар и отпустить его,
то он при ударе передаст свой импульс второму шару, второй — третьему и так
далее.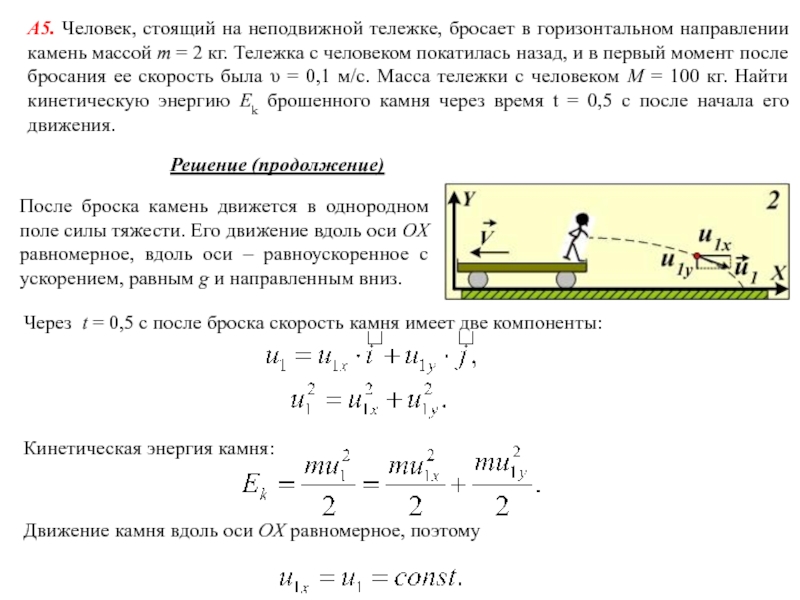 В результате можно наблюдать, что отскочит только один шар — тот, что
висит с противоположной стороны цепочки шаров, а все остальные шары останутся
на месте (рис. 40, б). Таким образом, импульс, потерянный при ударе первым шаром,
был передан последнему шару, суммарный же импульс системы не изменился.
Аналогичным образом можно отклонить в сторону и отпустить не один, а несколько
шаров. Тогда после удара с противоположной стороны в движение придёт столько же
шаров (рис. 40, в).
В результате можно наблюдать, что отскочит только один шар — тот, что
висит с противоположной стороны цепочки шаров, а все остальные шары останутся
на месте (рис. 40, б). Таким образом, импульс, потерянный при ударе первым шаром,
был передан последнему шару, суммарный же импульс системы не изменился.
Аналогичным образом можно отклонить в сторону и отпустить не один, а несколько
шаров. Тогда после удара с противоположной стороны в движение придёт столько же
шаров (рис. 40, в).
Закон сохранения импульса — это фундаментальный закон природы.
2. Выполнить тезисный конспект.
3. Вопросы для самопроверки
1. Чему равно изменение импульса тела, на которое действует сила?
2. Приведите пример опыта, подтверждающего, что изменение импульса тела зависит от времени действия силы.
3. Сформулируйте закон сохранения импульса.
4. Какую систему тел можно считать замкнутой.
4. Решить задачи.
1. До какой скорости мальчик разгонит стоящие на
снегу санки, прикладывая силу 10 Н в течение 0,5 с? Масса санок 2,5 кг,
действием силы трения пренебречь.
2. Вагон массой 25 т, двигаясь со скоростью 0,4 м/с, нагоняет второй такой же вагон, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после сцепки?
3. Пуля массой 10 г, двигаясь со скоростью 1000 м/с, попадает в неподвижную металлическую банку с песком и застревает в ней. С какой скоростью начнёт движение банка с пулей внутри, если её масса 1 кг?
Подборка по базе: Реферат Права автора в соответствии с законодательством РФ.docx, Саяси режим. Авторитаризм.pptx, реферат авторские права сми.docx, Попова Татьяна.docx, 2ЛЗ 14.10. Митюшина Татьяна Михайловна 121 а гр гигиена животных, Всемирная (Женевская) конвенция об авторском праве 1952 г.pptx, Анара Песталоции ғылыми еңбектеріне авторлық тұжырым.  docx, Чепегина Татьяна.docx, Фрідріх Дюрренматт як автор кримінального жанру.doc, Классификация принципов обучения современных авторов.docx docx, Чепегина Татьяна.docx, Фрідріх Дюрренматт як автор кримінального жанру.doc, Классификация принципов обучения современных авторов.docx12 Брусок массой 4 кг тянут по горизонтальной поверхности, с помощью пружины жесткостью 200 Нм, удлинение пружины 6 см. Найти коэффициент трения скольжения. С какой скоростью должно лететь тело массой 150 кг, чтобы его импульс был равен импульсу пули массой 18 г, летящей со скоростью 36 км/ч? Найти импульс грузового автомобиля массой 12 т, движущегося со скоростью 54 км/ч и легкого автомобиля массой 1,5 т, движущего 72 км/ч. Законы Ньютона, законы сохранения импульса и энергии Сформулируйте законы Ньютона Как, используя закон всемирного тяготения, вычислить значение ускорения свободного падения вблизи поверхности Земли и на некоторой высоте от нее. В чем состоит принцип независимости действия сил Что называют равнодействующей силой Как меняются законы Ньютона если ввести равнодействующую сил В чем состоит принцип относительности Галилея Чему равно изменение импульса тела, на которое действует сила Сформулируйте закон сохранения импульса.  Какие тела обладают кинетической энергией Какие тела обладают потенциальной энергией Сформулируйте закон сохранения полной механической энергии. Какие тела обладают кинетической энергией Какие тела обладают потенциальной энергией Сформулируйте закон сохранения полной механической энергии. 13 Каково удлинение металлического троса жесткостью 125 кН/м, если при буксировки легковой автомобиль массой 1 т движется с ускорением 0,5 мс Определите значение ускорения свободного падения вблизи поверхности Луны, считая ее массу равной Л 7,35 ∙ 10 та диаметр Л 3500 км. Во сколько рази как изменится сила тяжести, действующая на тело, если его поднять с поверхности Земли на высоту, равную двум радиусам Земли До какой скорости мальчик разгонит стоящие на снегу санки, прикладывая силу 10 Н в течении 0,5 с Масса санок 2,5 кг, действием силы трения пренебречь. Вагон массой 25 т, двигаясь со скоростью 0,4 мс, нагоняет второй такой же вагон, движущийся со скоростью 0,2 мс. Какова скорость вагонов после сцепки Пуля массой 10 г, двигаясь со скоростью 1000 мс, попадает в неподвижную металлическую банку с песком и застревает в ней. С какой скоростью начнет движение банка с пулей внутри, если ее масса 1 кг.  Какую работу совершит человек, равномерно передвигая тумбу по полу нам, если масса тумбы 50 кг, а коэффициент трения 0,02? Какую работу приходится совершать хозяину, удерживая собаку на дорожке длиной 10 м (см. рис Считать, что собака натягивает поводок с силой 30 На угол, который составляет натянутый поводок с горизонталью, 60 0 Какую работу совершит человек, равномерно передвигая тумбу по полу нам, если масса тумбы 50 кг, а коэффициент трения 0,02? Какую работу приходится совершать хозяину, удерживая собаку на дорожке длиной 10 м (см. рис Считать, что собака натягивает поводок с силой 30 На угол, который составляет натянутый поводок с горизонталью, 60 0? Какую начальную скорость нужно сообщить мячу, бросая его вниз с некоторой высоты чтобы мяч после удара о пол поднялся на высоту в 2 раза большую 14 Какую работу совершает мальчик массой 50 кг, поднимаясь по канату на высоту м Тело массой 2 кг, движущиеся на восток, тормозится постоянной силой в 10 Н, направленной на запад. Чему равно и куда направлено ускорение тела Коляска массой 10 кг движется на юг с ускорением 0,5 мс под действием двух сил, одна из которых 25 Н направлена на юг. Куда направлена и чему равна вторая сила, действующая на коляску На тело массой 5 кг действуют две силы первая 9 Н, вторая 12 Н, направленные на север и восток соответственно.  Чему равно и куда направлено ускорение тела Трактор, сила тяги которого на крюке 15 кН, сообщает прицепу ускорение 0,5 мс. Какое ускорение сообщит тому же прицепу трактор, развивающий тяговое усилие 60 кН? Сила 60 Н сообщает телу ускорение 0,8 мс. Какая сила сообщит этому телу ускорение 2 мс Тело массой 4 кг под действием некоторой силы приобрело ускорение 2 мс. Какое ускорение приобретает тело массой 10 кг под действием той же силы Порожний грузовой автомобиль массой 4 т начал движение с ускорением 0,3 мс. Какова масса груза, принятого автомобилем, если при той же силе тяги он трогается с места с ускорением 0,2 мс Заполните таблицу, где а ускорение, которое приобретает тело массой m под действием силы F. а Чему равно и куда направлено ускорение тела Трактор, сила тяги которого на крюке 15 кН, сообщает прицепу ускорение 0,5 мс. Какое ускорение сообщит тому же прицепу трактор, развивающий тяговое усилие 60 кН? Сила 60 Н сообщает телу ускорение 0,8 мс. Какая сила сообщит этому телу ускорение 2 мс Тело массой 4 кг под действием некоторой силы приобрело ускорение 2 мс. Какое ускорение приобретает тело массой 10 кг под действием той же силы Порожний грузовой автомобиль массой 4 т начал движение с ускорением 0,3 мс. Какова масса груза, принятого автомобилем, если при той же силе тяги он трогается с места с ускорением 0,2 мс Заполните таблицу, где а ускорение, которое приобретает тело массой m под действием силы F. а ? ? 0,4 мс 2 км/с 2 0,1 мс 5 см/с 2 m 8 кг 3 г 200 кг 10 г ? ? F 2 Н 6 мН ? ? 20 Н 1 кН С каким ускорением двигался при разбеге реактивный самолет массой 60 т, если сила тяги двигателей 90 кН? 15 Масса легкового автомобиля равна 2 та грузового 8 т.  Сравнить ускорения автомобилей, если сила тяги грузового автомобиля в 2 раза больше, чем легкового. Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстоянием. Найти силу их взаимного притяжения. Каково ускорение свободного падения на высоте, равной половине радиуса Земли Поезд массой 2000 т, двигаясь прямолинейно, увеличил скорость от 36 до 72 км/ч. Найти изменение импульса поезда. На вагонетку массой 50 кг, катящуюся по горизонтальному пути со скоростью 0,2 мс, насыпали сверху 200 кг щебня. Насколько, при этом уменьшилась скорость вагонетки Вагон массой т, движущийся со скоростью 0,3 мс, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 мс. Какова скорость вагонов после взаимодействия Какую работу совершает сила тяжести, действующая на дождевую каплю массой 20 мг, при ее падении с высоты 2 км Автомобиль массой 10 т движется под уклон по дороге, составляющей с горизонтом угол, равный 30 0 Сравнить ускорения автомобилей, если сила тяги грузового автомобиля в 2 раза больше, чем легкового. Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстоянием. Найти силу их взаимного притяжения. Каково ускорение свободного падения на высоте, равной половине радиуса Земли Поезд массой 2000 т, двигаясь прямолинейно, увеличил скорость от 36 до 72 км/ч. Найти изменение импульса поезда. На вагонетку массой 50 кг, катящуюся по горизонтальному пути со скоростью 0,2 мс, насыпали сверху 200 кг щебня. Насколько, при этом уменьшилась скорость вагонетки Вагон массой т, движущийся со скоростью 0,3 мс, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 мс. Какова скорость вагонов после взаимодействия Какую работу совершает сила тяжести, действующая на дождевую каплю массой 20 мг, при ее падении с высоты 2 км Автомобиль массой 10 т движется под уклон по дороге, составляющей с горизонтом угол, равный 30 0. Найти работу силы тяжести на пути 100 м.  Камень брошен вертикально вверх со скоростью Камень брошен вертикально вверх со скоростью ?????? 0 = 10 мс На какой высоте h кинетическая энергия камня равна его потенциальной энергии Для разрезывания сыра толщиной 15 см требуется усилие 40 Н. Какая при этом совершается работа Деревянный контейнер массой 200 кг равномерно передвинули по деревянному полу на расстоянием. Найдите работу, совершенную при таком перемещении. Коэффициент трения скольжения 0,5. |
Двигаться быстрее скорости света? — Нет ничего проще / Хабр
Теория относительности завораживает своими парадоксами. Все мы знаем про близнецов, про возможности засунуть длинный самолёт в короткий ящик. Сегодня каждый выпускник школы знает ответы на эти классические загадки, а уж студенты-физики и подавно считают, что тайн в специальной теории относительности для них не осталось.
Всё бы хорошо, если бы не удручающе обстоятельство — невозможность сверхсветовых скоростей. Неужели никак нельзя быстрее?! — думала я в детстве. А может быть можно?! Поэтому приглашаю вас на сеанс, уж и не знаю, чёрной или белой магии имени Альберта Эйнштейна с разоблачением в конце. Впрочем для тех, кому покажется мало, я приготовила ещё и задачку.
Впрочем для тех, кому покажется мало, я приготовила ещё и задачку.
UPD: Сутки спустя публикую решение. Много текста формул, графиков в конце.
К Альфе Центавра
Приглашаю вас занять места в нашем межзвёздном корабле, который направляется в сторону Альфы Центавра. От конечной точки маршрута нас отдаляют 4 световых года. Внимание, запускаем двигатели. Поехали! Для удобства пассажиров наш капитан установил такую тягу, чтобы мы ускорялись с величиной и ощущали привычную нам на Земле силу тяжести.
Вот мы уже прилично разогнались, пускай до половины скорости света . Зададим казалось несложный вопрос: с какой же скоростью мы будем приближаться к Альфа Центавра в нашей собственной (корабельной) системе отсчёта. Казалось бы всё просто, если мы летим со скоростью в неподвижной системе отсчёта Земли и Альфы Центавра, то и с нашей точки зрения мы приближаемся к цели со скоростью .
Тот, кто уже почувствовал подвох, совершенно прав. Ответ неверен! Тут надо сделать уточнение, под скоростью приближения к Альфа Центавра я называю изменение оставшегося расстояния до неё, делённое на промежуток времени, за который такое изменение произошло. Всё, разумеется, измеряется в нашей системе отсчёта, связанной с космическим кораблём.
Всё, разумеется, измеряется в нашей системе отсчёта, связанной с космическим кораблём.
Тут надо вспомнить, о лоренцевском сокращении длины. Ведь разогнавшись до половины скорости света мы обнаружим, что масштаб вдоль направления нашего движения сжался. Напомню формулу:
И теперь, если на скорости в половину скорости света мы измерим расстояние от Земли до Альфы Центавра, мы получил не 4 св. года, а всего лишь 3,46 св.года.
Получается, что только благодаря тому факту, что мы разогнались до мы уже уменьшили расстояние до конечной точки путешествия почти 0,54 св.года. А если мы будем не просто двигаться с большой скоростью, но ещё и ускоряться, то у масштабного фактора появится производная по времени, которая по сути тоже есть скорость приближения и плюсуется к .
Таким образом помимо к нашей обычной, я бы сказала классической, скорости добавляется ещё один член — динамическое сокращение длины оставшегося пути, которое возникает тогда и только тогда, когда есть ненулевое ускорение. Ну что же, возьмём карандаш и посчитаем.
Ну что же, возьмём карандаш и посчитаем.
Уже здесь мы видим, что первая частная производная — это скорость, просто скорость со знаком минус, коль скоро мы приближаемся к Альфе Центавра. А вот второе слагаемое — тот самый подвох, о котором, подозреваю, не все задумывались.
Чтобы найти производную скорости по времени во втором слагаемом, надо быть аккуратным, т.к. мы находимся в подвижной системе отсчёта. Проще всего на пальцах её вычислить из формулы сложения релятивистских скоростей. Пусть в момент времени мы движемся со скоростью , а через какой-то промежуток времени прирастили нашу скорость на . Результирующая скорость по формуле теории относительности будет
Теперь соберём вместе (2) и (3), причём производную от (3) надо взять при , т.к. мы рассматриваем малые приращения.
Полюбуемся на конечную формулу
Она удивительна! Если первый член — скорость — ограничен скоростью света, то второй член не ограничен ничем! Возьмите побольше и… второе слагаемое с лёгкостью может превысить .
— Что-что! — не поверят некоторые.
— Да-да, именно так, — отвечу я. — Оно может быть больше скорости света, больше двух скоростей света, больше 10 скоростей света. Перефразируя Архимеда, могу сказать: «дайте мне подходящую , и я обеспечу вам сколь угодно большую скорость.»
Что ж а давайте подставим числа, с числами всегда интереснее. Как мы помним, капитан установил ускорение , а скорость уже достигла . Тогда обнаружим, что при светового года, наша скорость приближения сравняется со скоростью света. Если же мы подставим световых года, то
Прописью: «три целых, три десятых скорости света».
Продолжаем удивляться
Давайте посмотрим ещё более внимательно на формулу (5). Ведь не обязательно садиться в релятивистский космический корабль.
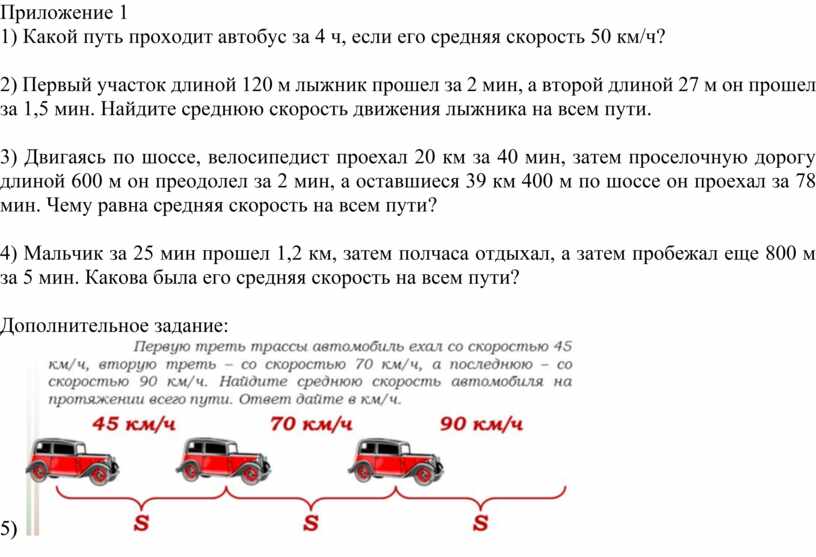 И скорость, и ускорение могут быть совсем маленькими. Всё дело в волшебной . Вы только вдумайтесь!
И скорость, и ускорение могут быть совсем маленькими. Всё дело в волшебной . Вы только вдумайтесь!Вот я села в машину и нажала на газ. У меня есть скорость и ускорение. И в этот самый момент я могу гарантировать, что где-то примерно сотне-другой миллионов световых лет впереди меня есть объекты, приближающиеся сейчас ко мне быстрее света. Для простоты я ещё не брала в расчёт скорость движения Земли по орбите вокруг Солнца, и Солнца вокруг центра Галактики. С их учётом объекты со сверхсветовой скоростью приближения окажутся уже совсем поблизости — не на космологических масштабах, а где-то на периферии нашей Галактики.
Получается, что невольно даже при минимальных ускорениях, например встав со стула, мы участвуем в сверхсветовом движении.
Удивляемся ещё
Посмотри на формулу (5) совсем-совсем пристально. Давайте узнаем не скорость приближения к Альфе Центавра, а наоборот скорость удаления от Земли. При достаточно большом , например, на полпути к цели, мы можем обнаружить, что к нам приближается и Земля, и Альфа Центавра.
 Оправившись от удивления, конечно можно догадаться, что виной всему сокращение длины, которое работает не только вперёд, но и назад. Пространство за кормой космического корабля сжимается быстрее, чем мы улетаем от точки старта.
Оправившись от удивления, конечно можно догадаться, что виной всему сокращение длины, которое работает не только вперёд, но и назад. Пространство за кормой космического корабля сжимается быстрее, чем мы улетаем от точки старта.Несложно понять и другой удивительный эффект. Ведь стоит изменить направление ускорения, как второе слагаемое в (5) тут же поменяет знак. Т.е. скорость приближения может запросто стать нулевой, а то и отрицательной. Хотя обычная скоростью у нас по прежнему будет направлена к Альфе Центавра.
Разоблачение
Надеюсь, я вас достаточно сбила с толку. Как же так, нас учили, что скорость света максимальна! Нельзя приближаться к чему-либо быстрее скорости света! Но здесь стоит обратить внимание на присказку к любому релятивистскому закону. Она есть в любом учебнике, но кажется, что только загромождает формулировку, хотя именно в ней вся «соль». Эта присказка гласит, что постулаты специальной теории относительности работают «в инерциальной системе отсчёта».
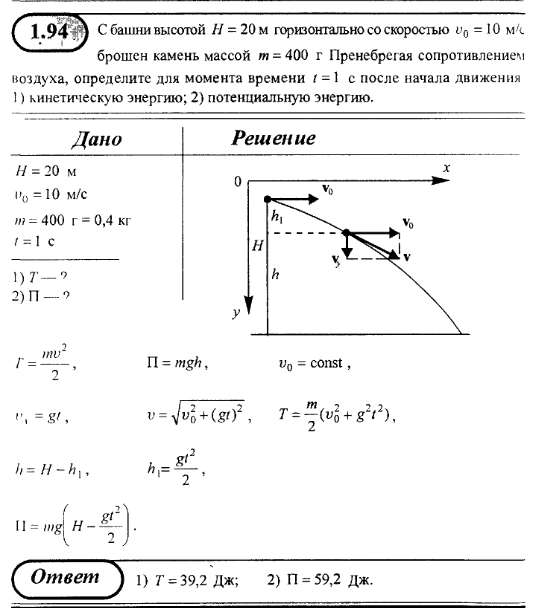
В неинерциальной системе отсчёта Эйнштейн нам ничего не гарантирует. Такие дела!
Тоже самое, чуть более подробно и чуть более сложноВ формуле (5) содержится расстояние . Когда оно равно нулю, т.е. когда мы пытаемся определить скорость локально относительно близких объектов, останется только первое слагаемое , которое, разумеется, не превышает световую скорость. Никаких проблем. И лишь на больших расстояниях, т.е. не локально, мы можем получить сверхсветовые скорости.Надо сказать, что вообще говоря, относительная скорость удалённых друг от друга объектов — понятие плохо определённое. Наше плоское пространство-время в ускоренной системе отсчёта выглядит искривлённым. Это знаменитый «лифт Эйнштейна» эквивалентный гравитационному полю. А сравнивать две векторные величины в искривлённом пространстве корректно, только когда они находятся в одной точке (в одном касательном пространстве из соответствующего векторного расслоения).
Кстати о нашем парадоксе сверхсветовой скорости можно рассуждать и по-другому, я бы сказала интегрально.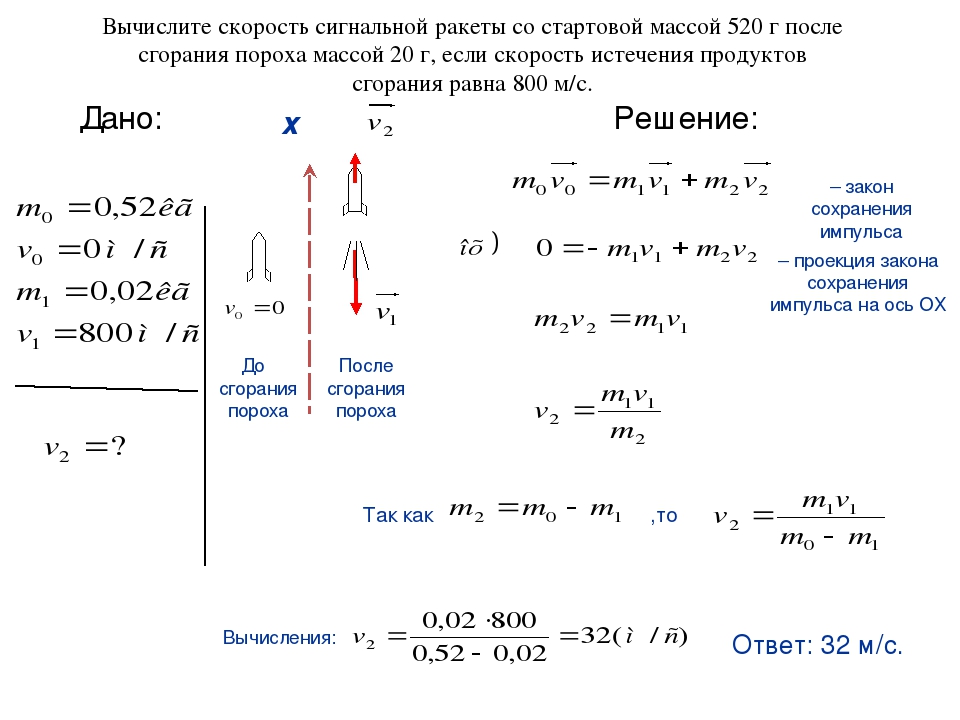 Ведь релятивистское путешествия к Альфе Центавра займёт по собственным часам космонавта гораздо меньше 4 лет, поэтому поделив изначальное расстояние на затраченное собственное время, мы получим эффективную скорость больше скорости света. По сути это тот же парадокс близнецов. Кому удобно, может именно так и понимать сверхсветовое перемещение.
Ведь релятивистское путешествия к Альфе Центавра займёт по собственным часам космонавта гораздо меньше 4 лет, поэтому поделив изначальное расстояние на затраченное собственное время, мы получим эффективную скорость больше скорости света. По сути это тот же парадокс близнецов. Кому удобно, может именно так и понимать сверхсветовое перемещение.
Вот и весь фокус. Ваша Капитанша Очевидность.
А напоследок я придумала вам домашнее задание или наброс для обсуждения в комментариях.
Задачка
Земляне и альфацентавры решили обменяться делегациями. С Земли стартовал космический корабль со скорость . Одновременно с ним с Альфы Центавра навстречу отправилась летающая тарелка инопланетян с той же скоростью.
Каково расстояние между кораблями в системе отсчёта корабля землян в момент старта, когда они находились у Земли и Альфы Центавра соответственно? Напишите ответ в комментариях.
UPD: Решение
Итак решение задачи. Сначала рассмотрим её качественно.

Договоримся, что часы на Альфе, Земле, ракете и тарелке синхронизованы (это было сделано заранее), и старт по всем четырём часам состоялся в 12:00.
Рассмотрим пространство время графически в покоящихся координатах . Земля находится в нуле, Альфа на расстоянии по оси . Мировая линия Альфы Центавра, очевидно, просто идёт вертикально вверх. Мировая линия тарелки идёт с наклоном влево, т.к. она вылетела из точки в направлении Земли.
Теперь на этом графике пририсуем оси координат системы отсчёта ракеты, стартовавшей с Земли. Как известно, такое преобразование системы координат (СК) называется бустом. При этом оси наклоняются симметрично относительно диагональной линии, которая показывает световой луч.
Я думаю, в этот момент вам уже всё стало понятно. Смотрите, ось пересекает мировые линии Альфы и летающей тарелки в разных точках. Что же произошло?
Удивительная вещь. Перед стартом с точки зрения ракеты и тарелка и Альфа находились в одной точке, а после набора скорости выясняется, что в движущеёся СК старт ракеты и тарелки не был одновременен. Тарелка, вдруг оказывается, стартовала раньше и успела немного приблизиться к нам. Поэтому сейчас в 12:00:01 по часам ракеты до тарелки уже ближе, чем до Альфы.
Тарелка, вдруг оказывается, стартовала раньше и успела немного приблизиться к нам. Поэтому сейчас в 12:00:01 по часам ракеты до тарелки уже ближе, чем до Альфы.
А если ракета разгонится ещё, она «перепрыгнет» в следующую СК, где тарелка ещё ближе. Причём такое приближение тарелки происходит только за счёт ускорения и динамического сжатия продольного масштаба (о чём собственно весь мой пост), а не продвижения ракеты в пространстве, т.к. ракета ещё по сути ничего и не успела пролететь. Это приближение тарелки, как раз и есть второй член в формуле (5).
Ну и кроме всего прочего надо учесть обычное лоренцевское сокращение расстояния. Сразу сообщу ответ, что при скоростях ракеты и тарелки по каждая расстояние
- между ракетой и Альфой: 3,46 св. года (обычное лоренцевское сокращение)
- между ракетой и тарелкой: 2,76 св. года
Кому интересно, давайте поколдуем с формулами в четырёхмерном пространствеТакого рода задачи удобно решать с помощью четырёхмерных векторов.
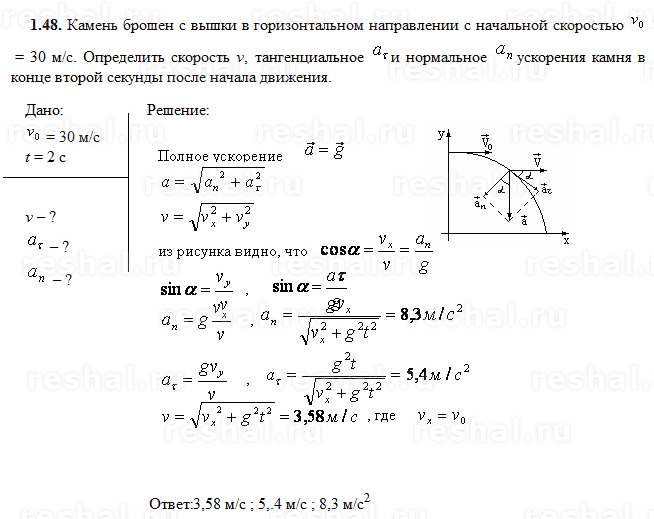 Бояться их не надо, всё делается при помощи самых обычных действий линейной алгебры. Тем более мы движемся только вдоль одной оси, поэтому от четырёх координат остаётся только две: и .
Бояться их не надо, всё делается при помощи самых обычных действий линейной алгебры. Тем более мы движемся только вдоль одной оси, поэтому от четырёх координат остаётся только две: и .Далее договоримся о простых обозначениях. Скорость света считаем равной единице. Мы, физики, всегда так делаем. 🙂 Ещё обычно единицей считаем постоянную Планка и гравитационную постоянную. Сути это не меняет, зато чертовски облегчает писанину.
Итак повсеместно присутствующий «релятивистский корень» обозначим гамма-фактором для компактности записей, где — скорость земной ракеты:
Теперь запишем в компонентах вектор :
Верхняя компонента — время, нижняя — пространственная координата. Корабли стартуют одновременно в неподвижной системе, поэтому верхняя составляющая вектора равна нулю.
Теперь найдём координаты точки в подвижной системе координат , т.е. . Для этого используем преобразование к движущейся системе отсчёта. Оно называется бустом и делается очень просто. Любой вектор надо умножить на матрицу буста
Умножаем:
Как мы видим, временная компонента этого вектора отрицательна. Это и значит, что точка с точки зрения движущеёся ракеты находится под осью , т.е. в прошлом (что и видно на рисунке выше).
Это и значит, что точка с точки зрения движущеёся ракеты находится под осью , т.е. в прошлом (что и видно на рисунке выше).
Найдём вектор в неподвижной системе. Временная компонента — некоторый неизвестный пока промежуток времени , пространственная — расстояние, на которое приближается тарелка за время , двигаясь со скоростью :
Теперь тот же самый вектор в системе
Найдём обычную векторную сумму
Почему эту сумму я приравняла справа к таком вектору? По определению точка находится на оси , поэтому временная компонента должна быть равна нулю, а пространственная компонента — это и будет то самое искомое расстояние от ракеты до тарелки. Отсюда получаем систему двух простых уравнений — приравниваем временные компоненты отдельно, пространственные отдельно.
Из первого уравнения определяем неизвестный параметр , подставляем его во второе уравнение и получаем . Позвольте опустить простые вычисления и сразу записать
Подставив , , получаем
Сборник задач — Приступа — Стр 2
67 С какой скоростью должна лететь хоккейная шайба массой 160
г, чтобы ее импульс был равен импульсу пули массой 8 г, летящей со скоростью 600 м/с?
68Какую силу в горизонтальном направлении необходимо приложить, что бы сдвинуть стоящий на горизонтальном полу ящик массой 0,5 кг, если коэффициент трения между ящиком и полом 0,05?
69На сколько сантиметров растянется пружина жесткостью 200
Н/м, если к ней подвесить груз массой 350 г?
70С какой скоростью должен ехать мотоциклист, чтобы его импульс был равен импульсу легкового автомобиля, движущегося со скоростью 54 км/ч, масса мотоцикла 250 кг, масса автомобиля1,5 т.
71Найти массу стального бруска, равномерно скользящего по горизонтальной поверхности под действием силы 30 Н. Сила направлена вдоль поверхности стола. Коэффициент трения скольжения равен 0,6.
72Деревянный брусок массой 10 кг тянут равномерно по горизонтальной поверхности с помощью пружины жесткостью 200
Н/м. Найдите удлинение пружины, если коэффициент трения
скольжения 0,9.
73Какие силы надо приложить к концам проволоки, жесткость которой 300 кН/м, чтобы растянуть на 3 мм?
74Две пружины разной длины, скрепленные одними концами,
растягивают за свободные концы руками. Пружина жесткостью 100
кН/м, удлинилась на 2 см. Какова, жесткость второй пружины, если ее
удлинение равно 0,2см?
75 На соревнованиях лошадей тяжелоупряжных пород одна из них перевезла груз массой 28 т. Найти коэффициент сопротивления, если сила тяги лошади 2,8кН.
11
76 Брусок массой 4 кг тянут по горизонтальной поверхности, с
помощью пружины жесткостью 200 Н/м, удлинение пружины 6 см.
Найти коэффициент трения скольжения.
77 С какой скоростью должно лететь тело массой 150 кг, что бы его импульс был равен импульсу пули массой 18 г, летящей со скоростью
36 км/ч?
78 Найти импульс грузового автомобиля массой 12 т, движущегося со скоростью 54 км/ч и легкого автомобиля массой 1,5 т, движущего
72 км/ч.
Законы Ньютона, законы сохранения импульса и энергии
79Сформулируйте законы Ньютона
80Как, используя закон всемирного тяготения, вычислить значение ускорения свободного падения вблизи поверхности Земли и на некоторой высоте от нее.
81В чем состоит принцип независимости действия сил?
82Что называют равнодействующей силой?
83Как меняются законы Ньютона если ввести равнодействующую
сил?
84В чем состоит принцип относительности Галилея?
85Чему равно изменение импульса тела, на которое действует
сила?
86Сформулируйте закон сохранения импульса.
87Какие тела обладают кинетической энергией?
88Какие тела обладают потенциальной энергией?
89Сформулируйте закон сохранения полной механической энергии.
12
90 Каково удлинение металлического троса жесткостью 125 кН/м,
если при буксировки легковой автомобиль массой 1 т движется с ускорением 0,5 м/с2?
91Определите значение ускорения свободного падения вблизи поверхности Луны, считая ее массу равной Л = 7,35 ∙ 1019т, а диаметр Л = 3500 км.
92Во сколько раз и как изменится сила тяжести, действующая на тело, если его поднять с поверхности Земли на высоту, равную двум радиусам Земли?
93До какой скорости мальчик разгонит стоящие на снегу санки,
прикладывая силу 10 Н в течении 0,5 с? Масса санок 2,5 кг, действием
силы трения пренебречь.
94Вагон массой 25 т, двигаясь со скоростью 0,4 м/с, нагоняет второй такой же вагон, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после сцепки?
95Пуля массой 10 г, двигаясь со скоростью 1000 м/с, попадает в неподвижную металлическую банку с песком и застревает в ней. С
какой скоростью начнет движение банка с пулей внутри, если ее масса
1 кг.
96Какую работу совершит человек, равномерно передвигая тумбу по полу на 2 м, если масса тумбы 50 кг, а коэффициент трения 0,02?
97Какую работу приходится совершать хозяину,
удерживая собаку на дорожке длиной 10 м (см.
рис.43)? Считать, что собака натягивает поводок с силой 30 Н, а угол, который составляет натянутый поводок с горизонталью, 600?
98 Какую начальную скорость нужно сообщить мячу, бросая его вниз с некоторой высоты h,чтобы мяч после удара о пол поднялся на высоту в 2 раза большую?
13
99Какую работу совершает мальчик массой 50 кг, поднимаясь по канату на высоту 3м?
100Тело массой 2 кг, движущиеся на восток, тормозится постоянной силой в 10 Н, направленной на запад. Чему равно и куда направлено ускорение тела?
101Коляска массой 10 кг движется на юг с ускорением 0,5 м/с2 под действием двух сил, одна из которых 25 Н направлена на юг. Куда направлена и чему равна вторая сила, действующая на коляску?
102На тело массой 5 кг действуют две силы: первая 9 Н, вторая 12
Н, направленные на север и восток соответственно. Чему равно и куда
Чему равно и куда
направлено ускорение тела?
103 Трактор, сила тяги которого на крюке 15 кН, сообщает прицепу ускорение 0,5 м/с2. Какое ускорение сообщит тому же прицепу трактор, развивающий тяговое усилие 60 кН?
104 Сила 60 Н сообщает телу ускорение 0,8 м/с2. Какая сила сообщит этому телу ускорение 2 м/с2?
105 Тело массой 4 кг под действием некоторой силы приобрело ускорение 2 м/с2. Какое ускорение приобретает тело массой 10 кг под действием той же силы?
106 Порожний грузовой автомобиль массой 4 т начал движение с ускорением 0,3 м/с2. Какова масса груза, принятого автомобилем, если при той же силе тяги он трогается с места с ускорением 0,2 м/с2?
107 Заполните таблицу, где а ускорение, которое приобретает тело массой m под действием силы F.
а | ? | ? | 0,4 м/с2 | 2 км/с2 | 0,1 м/с2 | 5 см/с2 |
|
|
|
|
|
|
|
m | 8 кг | 3 г | 200 кг | 10 г | ? | ? |
|
|
|
|
|
|
|
F | 2 Н | 6 мН | ? | ? | 20 Н | 1 кН |
|
|
|
|
|
|
|
108 С каким ускорением двигался при разбеге реактивный самолет массой 60 т, если сила тяги двигателей 90 кН?
14
109Масса легкового автомобиля равна 2 т, а грузового 8 т. Сравнить ускорения автомобилей, если сила тяги грузового автомобиля в 2 раза больше, чем легкового.
Сравнить ускорения автомобилей, если сила тяги грузового автомобиля в 2 раза больше, чем легкового.
110Космический корабль массой 8 т приблизился к орбитальной космической станции массой 20 т на расстояние 100 м. Найти силу их взаимного притяжения.
111Каково ускорение свободного падения на высоте, равной половине радиуса Земли?
112Поезд массой 2000 т, двигаясь прямолинейно, увеличил скорость от 36 до 72 км/ч. Найти изменение импульса поезда.
113На вагонетку массой 50 кг, катящуюся по горизонтальному пути со скоростью 0,2 м/с, насыпали сверху 200 кг щебня. На сколько, при этом уменьшилась скорость вагонетки?
114Вагон массой 20т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после взаимодействия?
115Какую работу совершает сила тяжести, действующая на дождевую каплю массой 20 мг, при ее падении с высоты 2 км?
116Автомобиль массой 10 т движется под уклон по дороге,
составляющей с горизонтом угол, равный 300. Найти работу силы тяжести на пути 100 м.
Найти работу силы тяжести на пути 100 м.
117 Камень брошен вертикально вверх со скоростью 0 = 10 м с.
На какой высоте h кинетическая энергия камня равна его потенциальной энергии?
118 Для разрезывания сыра толщиной 15 см требуется усилие 40 Н.
Какая при этом совершается работа?
119 Деревянный контейнер массой 200 кг равномерно передвинули по деревянному полу на расстояние 5 м. Найдите работу,
совершенную при таком перемещении. Коэффициент трения скольжения 0,5.
15
120Упряжка собак, протащив сани по горизонтальному пути длиной 10 км, совершает работу 980 кДж. Считая коэффициент трения равным 0,02, найдите массу саней.
121Найдите массу груза, если для его подъема на высоту 20 м
подъемник совершает работу 9,8 кДж.
122Шар массой 1 кг, летящий со скоростью 4 м/с, при ударе сжимает пружину. Найдите максимальную энергию сжатия пружины.
123Серьезной опасностью при межпланетных перелетах может стать столкновение космического корабля с небольшими скоростными метеоритами. Определите энергию микрометеорита массой 1 кг, движущегося со скоростью 60 км/с.
Определите энергию микрометеорита массой 1 кг, движущегося со скоростью 60 км/с.
124Энергия 7,4 ∙ 1016 Дж, выделяемая ураном-235, идет на ускорение космического корабля массой 3000 т. Какую максимальную скорость может набрать корабль?
16
Движение по наклонной плоскости
125На наклонной плоскости длиной 13 м и высотой 5 м лежит груз массой 26 кг.. Коэффициент трения равен 0,5. Какую силу надо приложить вдоль плоскости, чтобы втащить груз?
126Какую силу надо приложить для подъема вагонетки массой 600
кг по эстакаде с углом наклона 300, если коэффициент сопротивления движению равен 0,05?
127 На наклонной плоскости длиной 50 см и высотой 10 см покоится брусок массой 2 кг. При помощи динамометра,
расположенного параллельно плоскости, брусок сначала втащили вверх по наклонной плоскости, а затем стащили вниз. Найти разность показаний динамометра.
128На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить, чтобы удержать этот груз?
129На наклонной плоскости длиной 5 м и высотой 3 м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить, чтобы тянуть с ускорением 1 м/с2?
Какую силу, направленную вдоль плоскости, надо приложить, чтобы тянуть с ускорением 1 м/с2?
130Брусок массой 2 кг находится на наклонной плоскости с углом наклонна 300. Какую силу, направленную горизонтально, надо приложить к бруску, чтобы он двигался равномерно по наклонной плоскости? Коэффициент трения бруска о наклонную плоскость равен 0,3.
131Мальчик массой 22 кг, бегущий со скоростью 2,5 м/с,
вскакивает на неподвижную платформу массой 50 кг. Чему равна скорость платформы с мальчиком?
132 Из винтовки массой 5 кг, подвешенной на шнурах (рис.8),
вылетает пуля массой 4 г со скоростью 520 м/с. Чему равна скорость отдачи винтовки?
17
133Ракета выбрасывает раскаленные газы со скоростью 2000 м/с
относительно корабля. Чему равна сила тяги в момент старта, если каждую секунду выбрасывается масса, равная 100 кг?
134Вагон массой 30 т, движущийся по горизонтальному пути со скоростью 1,5 м/с, автоматически на ходу сцепляется с неподвижным вагоном массой 20 т. С какой скоростью будут двигаться вагоны после сцепки?
С какой скоростью будут двигаться вагоны после сцепки?
135Два неупругих шара массами 6 кг и 4 кг движутся со скоростями
8 м/с и 3 м/с соответственно, направленными вдоль одной прямой. С
какой скоростью они будут двигаться после абсолютно неупругого соударения, если: а) первый догоняет второй; б) шары движутся навстречу друг другу?
136Стрелковая пушка массой 200 кг установлена у края плоской крыши высокой башни. Пушка выпускает ядро массой 5 кг горизонтально. Ядро опускается на расстоянии 300 м от основания башни. Пушка, колеса которой вращаются без трения, тоже движется и падает на землю (рис.9). на каком расстоянии от основания башни пушка упадет на землю?
137Лодка находящаяся в стоячей воде. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние переместится лодка относительно воды, если масса человека 60 кг, масса лодки 120
кг и длина лодки 3 м? Сопротивлением воды пренебречь.
138 На поверхности озера находится лодка. Она перпендикулярна берегу и обращена к нему носом. Расстояние между носом лодки и берегом равно 0,75 м. В начальный момент лодка неподвижна.
Она перпендикулярна берегу и обращена к нему носом. Расстояние между носом лодки и берегом равно 0,75 м. В начальный момент лодка неподвижна.
Человек, находящийся в лодке, переходит с носа лодки на корму.
Причалит ли лодка к берегу за время движения человека, если ее
длина 2м? Масса лодки 140 кг, масса человека 60 кг.
139 Артиллеристы стреляют так, чтобы ядро попало в неприятельский лагерь. В момент вылета ядра из пушки на него
18
садится барон Мюнхгаузен, и поэтому ядро падает, не долетев до цели. Какую часть пути Мюнхгаузену придется идти пешком, чтобы добраться до неприятельского лагеря? Принять, что барон имеет массу в 5 раз большую, чем ядро. Посадку борона считать абсолютно неупругим ударом.
140На краю стола высотой h лежит маленький шарик массой m1. В
него попадает пуля массой m2, движущиеся горизонтально со скоростью v, направленной в центр шарика. Пуля застревает в нем. На каком расстоянии от стола по горизонтали упадет шарик на землю?
141Человек, стоящий на льду, ловит мяч массой 0,5 кг, который летит горизонтально со скоростью 20 м/с. С какой скоростью будет двигаться человек, когда поймает мяч? Масса человека 60 кг.
С какой скоростью будет двигаться человек, когда поймает мяч? Масса человека 60 кг.
142Человек массой 60 кг, стоящий на льду, бросает горизонтально мяч массой 0,5 кг со скоростью 15 м/с. Какую скорость приобретает человек сразу после броска?
143Пуля массой 5 г, летящая горизонтально со скоростью 500 м/с,
попадает в шар массой 0,5 кг и застревает в нем. Какую скорость
будет иметь шар сразу после попадания в него пули?
144С какой скоростью должна лететь пуля массой 5 г, чтобы после попадания е в шар массой 0,5 кг тот приобрел скорость 2 м/с? Пуля застревает в шаре.
145Снаряд массой 50 кг летит параллельно рельсам, попадает в движущуюся навстречу платформу с песком и застревает в нем. Масса платформы с песком 20 т. С какой скоростью должен лететь снаряд,
чтобы платформа остановилась?
146 Снаряд массой 50 кг летит параллельно рельсам и попадает в движущуюся ему навстречу платформу с песком массой 20 т. С какой скоростью летел снаряд, если сразу после того, как он застрял в песке,
платформа стала двигаться в противоположную строну со скоростью
1 м/с? В момент столкновения скорость тележки была равна 2 м/с.
19
147 Тело брошено со скоростью 20 м/с под углом 300 к горизонту.
Определите его скорость на высоте 1 м.
148Пружинное ружье выстреливает шарик вертикально вверх на высоту 30 см, если пружина сжата на 1 см. Какова начальная скорость полета шарика? На какую высоту поднимается шарик, если эту пружину сжать на 3 см?
149С какой начальной скоростью надо бросить вниз мяч с высоты 2
м, чтобы он подпрыгнул на высоту 4 м? Считать удар о землю абсолютно упругим.
150 Тележка на «американских горках» начинает движение без начальной скорости в наивысшей точке траектории на высоте 20 м
над землей. Она резко опускается вниз до высоты 2 м и затем круто взмывает вверх до вершины следующей горы, которая расположена на высоте 15 м. Какова скорость тележки в желобе на высоте 2 м и на 15-
метровой вершине, если потери энергии и трением можно пренебречь?
151 Стрела вылетает из арбалета вертикально вверх со скоростью 60
м/с. На какую высоту поднимается стрела, если ее масса равна 200 г?
На какую высоту поднимается стрела вдвое большей массы?
Потерями энергии пренебречь.
152При подготовке игрушечного пистолета к выстрелу пружину жесткостью 800 Н/м сжали на 5 см. Какую скорость приобретает пуля массой 20 г при выстреле в горизонтальном направлении?
153Хоккейная шайба скользит 5 м, если при броске ей сообщают начальную скорость 2 м/с. Какой путь она пройдет, если ей сообщить начальную скорость 4 м/с?
154Пуля, вылетевшая из винтовки со скоростью 1000 м/с, упала на землю со скоростью 500 м/с. Какая работа была совершена силой сопротивления воздуха, если масса пули 10 г?
20
4,3 Второй закон движения Ньютона
Применение второго закона Ньютона
Прежде чем применять второй закон Ньютона, важно рассмотреть единицы измерения.
Уравнение Fnet = ma Fnet = ma используется для определения единиц силы в терминах трех основных единиц массы, длины и времени (напомним, что ускорение состоит из единиц длины, разделенных на квадрат времени). Единица силы в системе СИ называется ньютон (сокращенно Н) и представляет собой силу, необходимую для ускорения системы массой 1 кг со скоростью 1 м / с 2 . То есть, поскольку Fnet = ma, Fnet = ma, мы имеем
То есть, поскольку Fnet = ma, Fnet = ma, мы имеем
Одним из наиболее важных применений второго закона Ньютона является вычисление веса (также известного как сила тяжести), который математически обычно представляется как W . Когда люди говорят о гравитации, они не всегда понимают, что это ускорение. Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что чистая внешняя сила, действующая на объект, ответственна за его ускорение.Если сопротивление воздуха незначительно, чистая внешняя сила на падающий объект — это только сила тяжести (т. Е. Вес объекта).
Вес может быть представлен вектором, потому что он имеет направление. Вниз определяется как направление, в котором тянет сила тяжести, поэтому вес обычно считается направленной вниз силой. Используя второй закон Ньютона, мы можем вычислить уравнение веса.
Рассмотрим объект массой м , падающий на Землю. Он испытывает только силу тяжести (т.е., гравитационная сила или вес), который представлен вторым законом У. Ньютона, согласно которому Fnet = ma. Fnet = ma. Поскольку единственная сила, действующая на объект, — это сила тяжести, мы имеем Fnet = W. Fnet = W. Мы знаем, что ускорение объекта под действием силы тяжести составляет g , поэтому мы имеем a = g. а = г. Подставляя эти два выражения во второй закон Ньютона, получаем
Он испытывает только силу тяжести (т.е., гравитационная сила или вес), который представлен вторым законом У. Ньютона, согласно которому Fnet = ma. Fnet = ma. Поскольку единственная сила, действующая на объект, — это сила тяжести, мы имеем Fnet = W. Fnet = W. Мы знаем, что ускорение объекта под действием силы тяжести составляет g , поэтому мы имеем a = g. а = г. Подставляя эти два выражения во второй закон Ньютона, получаем
Это уравнение для веса — силы тяжести на массу м . На Земле g = 9,80 м / с2, g = 9.80 м / с2, поэтому вес (без учета направления веса) объекта массой 1,0 кг на Земле составляет
4,8 Вт = mg = (1,0 кг) (9,80 м / с2) = 9,8 NW = mg = ( 1,0 кг) (9,80 м / с2) = 9,8 Н.Хотя в большинстве стран мира в качестве единицы силы используется ньютон, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.
Напомним, что хотя сила тяжести действует вниз, ей можно присвоить положительное или отрицательное значение, в зависимости от того, какое положительное направление находится в выбранной вами системе координат. Обязательно учтите это при решении задач с весом. Когда направление вниз считается отрицательным, как это часто бывает, ускорение свободного падения становится равным
Обязательно учтите это при решении задач с весом. Когда направление вниз считается отрицательным, как это часто бывает, ускорение свободного падения становится равным
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении. В этом случае единственной силой, действующей на объект, является сила тяжести. На поверхности Земли, когда объекты падают вниз к Земле, они никогда не находятся в истинном свободном падении, потому что всегда существует некоторая восходящая сила из-за сопротивления воздуха, которое действует на объект (и есть также сила плавучести воздуха, которая аналогична сила плавучести в воде, которая удерживает лодки на плаву).
Гравитация незначительно меняется на поверхности Земли, поэтому вес объекта очень слабо зависит от его местоположения на Земле. Вес резко меняется от поверхности Земли. Например, на Луне ускорение свободного падения составляет всего 1,67 м / с 2 . Поскольку вес зависит от силы тяжести, масса в 1,0 кг весит 9,8 Н на Земле и всего около 1,7 Н на Луне.
Поскольку вес зависит от силы тяжести, масса в 1,0 кг весит 9,8 Н на Земле и всего около 1,7 Н на Луне.
Важно помнить, что вес и масса очень разные, хотя они тесно связаны.Масса — это количество вещества (сколько составляет ) в объекте и не меняется, но вес — это сила тяжести на объекте, пропорциональная силе тяжести. Их легко спутать, потому что наш опыт ограничен Землей, а вес объекта по существу одинаков, независимо от того, где вы находитесь на Земле. Путаницу усугубляет то, что термины масса и вес часто используются как синонимы в повседневном языке; например, в наших медицинских записях наш вес часто указывается в килограммах, но никогда в правильных единицах измерения — ньютонах.
Snap Lab
Масса и вес
В этом упражнении вы будете использовать весы для определения массы и веса.
- Что измеряют весы для ванной?
- Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает.
 Весы содержат пружины, которые сжимаются пропорционально вашему весу — подобно резиновым лентам, расширяющимся при натяжении.
Весы содержат пружины, которые сжимаются пропорционально вашему весу — подобно резиновым лентам, расширяющимся при натяжении. - Пружины определяют ваш вес (при условии, что вы не ускоряетесь).Это сила в ньютонах (или фунтах). В большинстве стран измерение теперь делится на 9,80, чтобы получить значение в килограммах, что соответствует массе. Весы определяют вес, но откалиброваны для отображения массы.
- Если бы вы отправились на Луну и встали на свои весы, обнаружила бы она ту же массу , что и на Земле?
Проверка захвата
Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему?
- Показание увеличивается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, действующую в направлении вашего веса.
- Показание увеличивается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, действующую в направлении, противоположном вашему весу.

- Показание уменьшается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, действующую в направлении вашего веса.
- Показание уменьшается, потому что часть вашего веса приложена к столу, и стол оказывает на вас соответствующую силу, которая действует в направлении, противоположном вашему весу.
Советы для успеха
Только чистая внешняя сила влияет на ускорение объекта. Если на объект действует более одной силы, и вы вычисляете ускорение, используя только одну из этих сил, вы не получите правильное ускорение для этого объекта.
Watch Physics
Второй закон движения Ньютона
В этом видео рассматривается второй закон движения Ньютона и то, как чистая внешняя сила и ускорение связаны друг с другом и с массой.Он также охватывает единицы силы, массы и ускорения и рассматривает отработанный пример.
Проверка захвата
Верно или неверно. Если вы хотите уменьшить ускорение объекта до половины от его первоначального значения, тогда вам необходимо уменьшить чистую внешнюю силу вдвое.
- Истинно
- Ложь
Рабочий пример
Какое ускорение может вызвать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н, параллельную земле.Масса косилки 240 кг. Какое у него ускорение?
Стратегия
Поскольку даны F net и м , ускорение можно рассчитать непосредственно из второго закона Ньютона: F net = м a .
Решение
Решая второй закон Ньютона для ускорения, мы находим, что величина ускорения, a , равна a = Fnetm. а = Fnetm. Ввод данных значений чистой внешней силы и массы дает
а = Fnetm. Ввод данных значений чистой внешней силы и массы дает
Вставив единицы измерения кг⋅м / с2 кг⋅м / с2 для N, получаем
4,10a = 51 кг⋅м / с 2240 кг = 0,21 м / с2.a = 51 кг⋅м / s2240 кг = 0,21 м / с2.Обсуждение
Ускорение происходит в том же направлении, что и чистая внешняя сила, которая параллельна земле и направо. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению, потому что нам дано, что чистая внешняя сила направлена в том направлении, в котором человек толкает.Кроме того, вертикальные силы должны нейтрализоваться, если нет ускорения в вертикальном направлении (косилка движется только горизонтально). Найденное ускорение приемлемо для человека, толкающего косилку; скорость косилки должна увеличиваться на 0,21 м / с каждую секунду, что возможно. Время, в течение которого газонокосилка разгоняется, не будет очень долгим, потому что скоро человек достигнет максимальной скорости. На этом этапе человек может толкать немного меньше, потому что ему нужно только преодолеть трение.
Время, в течение которого газонокосилка разгоняется, не будет очень долгим, потому что скоро человек достигнет максимальной скорости. На этом этапе человек может толкать немного меньше, потому что ему нужно только преодолеть трение.
Рабочий пример
Какая ракетная тяга ускоряет эти салазки?
До пилотируемых космических полетов ракетные сани использовались для проверки самолетов, ракетного оборудования и физиологических воздействий на людей при высоких ускорениях.Ракетные сани представляли собой платформу, установленную на одном или двух рельсах и приводимую в движение несколькими ракетами. Вычислите величину силы, прилагаемой каждой ракетой, которая называется ее тягой, T , для четырехракетной двигательной установки, показанной ниже. Начальное ускорение салазок составляет 49 м / с2, 49 м / с2, масса системы — 2100 кг, сила трения, препятствующая движению, — 650 Н.
Стратегия
Интересующая система — ракетные сани. Хотя силы действуют на систему вертикально, они должны нейтрализоваться, поскольку система не ускоряется вертикально.Остается учитывать только горизонтальные силы. Мы назначим направление вправо как положительное. См. Диаграмму свободного тела на рис. 4.8.
Хотя силы действуют на систему вертикально, они должны нейтрализоваться, поскольку система не ускоряется вертикально.Остается учитывать только горизонтальные силы. Мы назначим направление вправо как положительное. См. Диаграмму свободного тела на рис. 4.8.
Решение
Начнем со второго закона Ньютона и ищем способы определить тягу T двигателей. Поскольку все силы и ускорения линейны, нам нужно учитывать только величины этих величин в расчетах. Начнем с
, где Fnet Fnet — чистая внешняя сила в горизонтальном направлении.Из рисунка 4.8 видно, что тяга двигателя в одном направлении (которое мы называем положительным направлением), тогда как трение противодействует тяге. В форме уравнения чистая внешняя сила равна
. 4.12Fnet = 4T − f .Fnet = 4T − f.Второй закон Ньютона говорит нам, что F net = м a , поэтому мы получаем
4.13ma = 4T − f .ma = 4T − f.
После небольшой алгебры решаем общую тягу 4 T :
4.144T = ma + f, 4T = ma + f,, что означает, что индивидуальная тяга равна
4.15Т = ма + f4 .Т = ма + f4.Вставка известных значений дает
4,16T = (2100 кг) (49 м / с2) +650 N4 = 2,6 × 104 Н.Т = (2100 кг) (49 м / с2) +650 N4 = 2,6 × 104 Н.Обсуждение
Цифры довольно большие, поэтому результат может вас удивить. Подобные эксперименты проводились в начале 1960-х годов, чтобы проверить пределы человеческой выносливости и проверить устройство, предназначенное для защиты летчиков-истребителей от аварийных катапультирований. Были получены скорости 1000 км / ч, с ускорением 45 g .(Напомним, что g, ускорение свободного падения, составляет 9,80 м / с2. 9,80 м / с2. Ускорение 45 g составляет 45 × 9,80 м / с2, 45 × 9,80 м / с2, что составляет примерно 440 м / с2. s2. 440 м / с2.) Живые предметы больше не используются, и теперь с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч. В этом примере, как и в предыдущем примере, интересующая система ясна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение и что этот выбор не всегда очевиден.
В этом примере, как и в предыдущем примере, интересующая система ясна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение и что этот выбор не всегда очевиден.
1D Kinematics Review — с ответами № 4
Перейдите к:
Обзорная сессия Домашняя страница — Листинг1D Kinematics — Домашняя страница || Версия для печати || Вопросы и ссылки
Ответы на вопросы: # 1-7 || №8- №28 || # 29- # 42 || # 43- # 50
[# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]Часть E: вычислительные проблемы
43.Определите ускорение (в м / с 2 ) объекта, который ….
- движется по прямой с постоянной скоростью 20,0 м / с в течение 12,0 секунд
- изменяет свою скорость с 12,1 до 23,5 м / с за 7,81 секунды.

- изменяет свою скорость с 0,0 миль / ч до 60,0 миль / ч за 4,20 секунды.
- разгоняется с 33,4 до 18,9 м / с на расстоянии 109 м.
Ответ: См. Ответы, пояснения и расчеты ниже.
а. Если скорость и направление объекта постоянны, то ускорение равно 0 м / с 2 .
г. Ускорение — это отношение изменения скорости за время:
a = (Изменение скорости) / t = (23,5 м / с — 12,1 м / с) / (7,81 с) = 1,46 м / с 2 .г. Ускорение — это отношение изменения скорости за время:
a = (Изменение скорости) / t = (60,0 миль / час — 0,0 миль / час) / (4,20 с) = 14,3 миль / час / с .14.3 мили / час / с * (1,0 м / с) / (2,24 миль / час) = 6,38 м / с 2 .
г. Значение ускорения также можно рассчитать с помощью кинематических уравнений, если известны три другие кинематические величины. В этом случае известная информация: v o = 33,4 м / с; v f = 18,9 м / с; и d = 109 м. Используя уравнение v f 2 = v o 2 + 2 * a * d, можно вычислить ускорение.
Используя уравнение v f 2 = v o 2 + 2 * a * d, можно вычислить ускорение.
44. Определите величину перемещения (в метрах) объекта, который ….
- перемещается из Hither в Yon (со средней скоростью 28,0 м / с), а затем обратно в Hither (со средней скоростью 28,0 м / с), если оба пути вперед и назад занимают 46 минут каждый.
- движется с постоянной скоростью 8.30 м / с по прямой в течение 15,0 секунд.
- замедляется со скоростью -4,35 м / с / с со скорости 38,1 м / с до скорости 17,6 м / с
- ускоряется из состояния покоя со скоростью 3,67 м / с 2 за 12,1 секунды
- движется со скоростью 12,2 м / с, а затем ускоряется со скоростью +1,88 м / с 2 в течение 17,0 секунд
Ответ: См. Ответы, пояснения и расчеты ниже.
Ответы, пояснения и расчеты ниже.
а. Поскольку это поездка туда и обратно, общее смещение составляет 0 м.
г. Поскольку скорость постоянна, смещение можно найти, умножив скорость на время.
d = v * t = (8,30 м / с) * (15,0 с) = 125 мг. Значение смещения также можно рассчитать с помощью кинематических уравнений, если известны три другие кинематические величины. В этом случае известная информация: v o = 38,1 м / с; v f = 17,6 м / с; и a = -4,35 м / с / с. Используя уравнение v f 2 = v o 2 + 2 * a * d, можно вычислить смещение.
d = (v f 2 — v o 2 ) / (2 * a) = [(17,6 м / с) 2 — (38,1 м / с) 2 ] / (2 * -4,35 м / с / с) = 131 м . г. Значение смещения можно рассчитать с использованием других кинематических уравнений, если известен другой набор кинематических величин. Здесь мы знаем, что: v o = 0,0 м / с; t = 12,1 с; и a = 3,67 м / с / с. Используя уравнение d = v o * t + 0,5 * a * t 2 , можно вычислить смещение.
Используя уравнение d = v o * t + 0,5 * a * t 2 , можно вычислить смещение.
e. Здесь величина смещения рассчитывается с использованием того же кинематического уравнения. Мы знаем, что: v o = 12,2 м / с; t = 17,0 с; и a = 1,88 м / с / с. Используя уравнение d = v o * t + 0,5 * a * t 2 , можно вычислить смещение.
d = (12,2 м / с) * (17,0 с) + 0,5 * (1,88 м / с / с) * (17,0 с) 2 = 479 м . [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]45.Заяц спит на локации в 1200 м от финиша. Черепаха обгоняет его с постоянной скоростью 5,0 см / с. Если заяц наконец просыпается через 6,5 часов, то какое минимальное ускорение (предполагаемое постоянное) должно быть у него, чтобы обогнать черепаху до финиша.
Ответ: 0,0067 м / с 2
Как и во многих других словесных задачах по физике, есть несколько путей к окончательному ответу. Решение всех таких проблем включает в себя обдумывание и хорошие стратегии решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. Д.).
Решение всех таких проблем включает в себя обдумывание и хорошие стратегии решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. Д.).
Черепаха, двигаясь с постоянной скоростью, преодолеет 1200 м за:
t черепаха = d / v черепаха = (1200 м) / (0,050 м / с) = 24000 с = 6,666 … часовЗаяц будет спать 6,5 часов (23400 с) перед стартом, поэтому у него будет всего 0,1666 … часов (600 с), чтобы разогнаться до финиша. Таким образом, ускорение зайца можно определить с помощью кинематического уравнения. Известная информация о движении зайца: t = 600 с; d = 1200 м; v o = 0 м / с.Лучшее уравнение: d = v o * t + 0,5 * a * t 2 . Член v o * t отменяется, и уравнение может быть алгебраически преобразовано и решено для a:
a = 2 * d / t 2 = 2 * (1200 м) / (600 с) 2 = 0,0067 м / с 2 . [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]
46. Золотая машина движется в точке 12.0 м / с проезжает Green Car , а Green Car стоит на светофоре. Green Car немедленно ускоряется со скоростью +1,80 м / с / с в течение 11,0 секунд, а затем поддерживает постоянную скорость. Через какое время (относительно начального времени старта) Green Car должен проехать, прежде чем догнать Gold Car .
Золотая машина движется в точке 12.0 м / с проезжает Green Car , а Green Car стоит на светофоре. Green Car немедленно ускоряется со скоростью +1,80 м / с / с в течение 11,0 секунд, а затем поддерживает постоянную скорость. Через какое время (относительно начального времени старта) Green Car должен проехать, прежде чем догнать Gold Car .
Ответ: 14,0 с
(Как упоминалось в предыдущей задаче …) Как и во многих других словесных задачах по физике, существует несколько путей к окончательному ответу.Решение всех таких проблем включает обдумывание и хорошие стратегии решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. Д.).
Здесь золотой автомобиль движется с постоянной скоростью в течение т секунд (где т — общее время в пути для обеих машин). Расстояние, пройденное золотой машиной, определяется кинематическим уравнением d = v o * t + 0,5 * a * t 2 . Второй член отменяется, и расстояние можно выразить как
Второй член отменяется, и расстояние можно выразить как
d золото = 12,0 * t
Для зеленой машины есть период ускорения, а затем период постоянной скорости. Расстояние, пройденное за период ускорения (d 1 зеленый ), находится из того же кинематического уравнения. Для зеленой машины первый член отменяется, и расстояние равно
. d 1 зеленый = v o * t + 0,5 * a * t 2 = 0,5 * (1,80 м / с 2 ) * (11.0 с) 2 , илиd 1 зеленый = 108,9 м
После того, как зеленый автомобиль разогнался в течение 11 секунд, он поддерживает постоянную скорость в течение оставшегося времени, определяемого выражением t — 11 с. Скорость, с которой зеленый автомобиль движется за это время, можно вычислить по формуле:
v f зеленый = v o + a * t = (1,80 м / с 2 ) * (11,0 с) = 19,8 м / с Расстояние, пройденное зеленым автомобилем во время этого участка движения с постоянной скоростью (d 2green ), можно вычислить с помощью кинематического уравнения. d = v o * t + 0,5 * a * t 2 . Второй член отменяется, и расстояние можно выразить как
d = v o * t + 0,5 * a * t 2 . Второй член отменяется, и расстояние можно выразить как
д 2зеленый = 19,8 * т — 217,8
Итак, общее расстояние, пройденное зеленой машиной, определяется выражением:
d зеленый = d 1 зеленый + d 2 зеленый = 108,9 + 19,8 * t — 217,8d зеленый = 19.8 * т — 108,9
Когда зеленая машина догонит золотую, их пройденное расстояние будет таким же. Таким образом, время t можно определить, задав два выражения для расстояния равными друг другу и решив для t.
12,0 * т = 19,8 * т — 108,9108,9 = 7,80 * т
т = (108,9) / (7,80)
t = 13,96 с = 14,0 с
[# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50] 47.Ima Rilla Saari движется со скоростью 28,0 м / с по Лейк-авеню и через лесной заповедник. Она замечает, как олень прыгает на дорогу в 62,0 м перед ней. Има сначала реагирует на событие, затем нажимает на тормоза и замедляет скорость -8,10 м / с 2 , и в конечном итоге останавливает пикометр перед замороженным оленем . Каково время реакции Имы ? (т.е. сколько времени потребовалось Има, чтобы отреагировать на событие до замедления?)
Она замечает, как олень прыгает на дорогу в 62,0 м перед ней. Има сначала реагирует на событие, затем нажимает на тормоза и замедляет скорость -8,10 м / с 2 , и в конечном итоге останавливает пикометр перед замороженным оленем . Каково время реакции Имы ? (т.е. сколько времени потребовалось Има, чтобы отреагировать на событие до замедления?)
Ответ: 0.486 с
Общее пройденное расстояние Имы (62,0 м) можно разделить на два сегмента — расстояние реакции (d rxn ) и тормозной путь (d торможение ). Расстояние реакции — это расстояние, которое Ima проходит до торможения; она будет двигаться с постоянной скоростью в это время т rxn . Тормозной путь — это расстояние, которое Има проходит, когда ее нога нажимает на тормоз, и она замедляется с 28,0 м / с до 0,0 м / с. Сначала можно рассчитать тормозной путь, используя следующее кинематическое уравнение: v f 2 = v o 2 + 2 * a * d. Известная информация для этого периода торможения: v o = 28 м / с; v f = 0 м / с; и a = -8,10 м / с / с. Замены и решения показаны ниже.
Известная информация для этого периода торможения: v o = 28 м / с; v f = 0 м / с; и a = -8,10 м / с / с. Замены и решения показаны ниже.
Так как машине Имы требуется 48,40 м для торможения, она может проехать максимум 13,6 м за время реакции. Связь между временем реакции, скоростью и расстоянием реакции определяется уравнением
d rxn = v * t rxnЗамена 13.6 м для d rxn и 28,0 м / с для v, время реакции можно вычислить:
t rxn = (13,6 м) / (28,0 м / с) = 0,486 с [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50] 48. Двухступенчатая ракета ускоряется из состояния покоя со скоростью +3,57 м / с / с за 6,82 секунды. Затем он ускоряется со скоростью +2,98 м / с / с еще 5,90 секунды. После второй стадии он переходит в состояние свободного падения. Определить:
После второй стадии он переходит в состояние свободного падения. Определить:
- максимальная скорость
- максимальная высота
- высота ракеты после 20.0 секунд
- общее время нахождения ракеты в воздухе (при условии, что она запущена с земли)
Ответ: См. Ответы и пояснения ниже.
К этой проблеме можно подойти, используя либо график скорости-времени, либо кинематические уравнения (или их комбинацию). Каким бы ни был подход, необходимо обязательно разбить многоступенчатое движение на три различных периода ускорения. Использование кинематических уравнений подходит только для постоянных периодов ускорения.По этой причине сложное движение должно быть разбито на периоды времени, в течение которых ускорение является постоянным. Эти три периода времени можно увидеть на графике скорость-время тремя линиями с явно разным наклоном. На диаграмме справа показано движение; помечены стратегические точки. Эти моменты будут упомянуты в решениях ниже.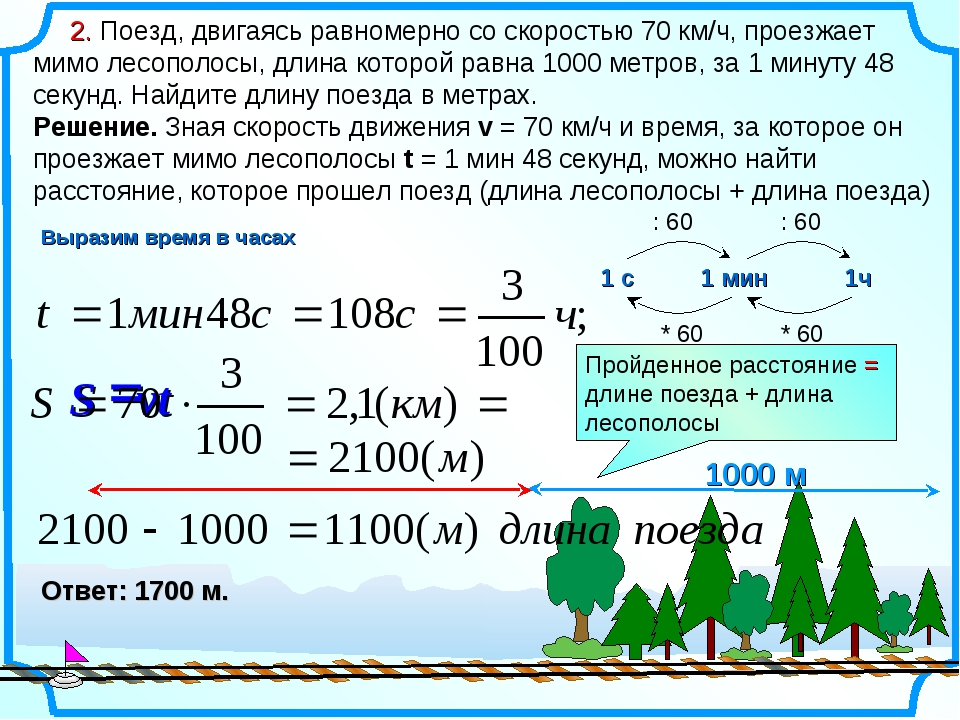 График скорости-времени, представленный ниже, будет использоваться во всем решении; Обратите внимание, что на графике обозначены те же самые стратегические точки.
График скорости-времени, представленный ниже, будет использоваться во всем решении; Обратите внимание, что на графике обозначены те же самые стратегические точки.
а. Максимальная скорость достигается после второй ступени или периода разгона (точка C). По истечении этого времени движущаяся вверх ракета начинает замедляться, поскольку гравитация становится единственной силой, действующей на нее. Для определения этой скорости (v c ) кинематическое уравнение v f = v o + a * t будет использоваться дважды — один раз для каждого периода ускорения.
Первая ступень: v B = v A + a * t = 0 м / с + (3,57 м / с / с) * (6,82 с) = 24,3 м / сВторой этап: v C = v B + a * t = 24.3 м / с + (2,98 м / с / с) * (5,90 с) = 41,9 м / с
г. Максимальная высота достигается в точке D, через некоторое время после того, как вторая ступень остановится и у ракеты закончится пар . Скорость в этой точке равна 0 м / с (это пик траектории). Высота в этой точке — это суммарное расстояние, пройденное от t = 0 с до t = t D . Это расстояние — это расстояние для первой ступени, второй ступени и периода замедления (от C до D).Эти расстояния соответствуют площади на графике v-t; на графике они обозначены A 1 , A 2 и A 3 . Они рассчитаны и суммированы ниже.
Скорость в этой точке равна 0 м / с (это пик траектории). Высота в этой точке — это суммарное расстояние, пройденное от t = 0 с до t = t D . Это расстояние — это расстояние для первой ступени, второй ступени и периода замедления (от C до D).Эти расстояния соответствуют площади на графике v-t; на графике они обозначены A 1 , A 2 и A 3 . Они рассчитаны и суммированы ниже.
A 2 = b * h + 0,5 * b * h (треугольник на вершине квадрата)
A 2 = (24,3 м / с) * (5,9 с) + 0,5 * (41,9 м / с — 24,3 м / с) * (5,9 с) = 195,42 м
Необходимо знать время от точки C до точки D, чтобы определить A 3 .Это время можно определить с помощью кинематического уравнения v f = v o + a * t, для которого v f = 0 м / с и v o = 41,9 м / с и a = -9,8 м / с. SS.
v D = v C + a * t0 м / с = 41,9 м / с + (-9,8 м / с / с) * t
t = 4,28 с
Теперь A 3 можно определить с помощью графика v-t.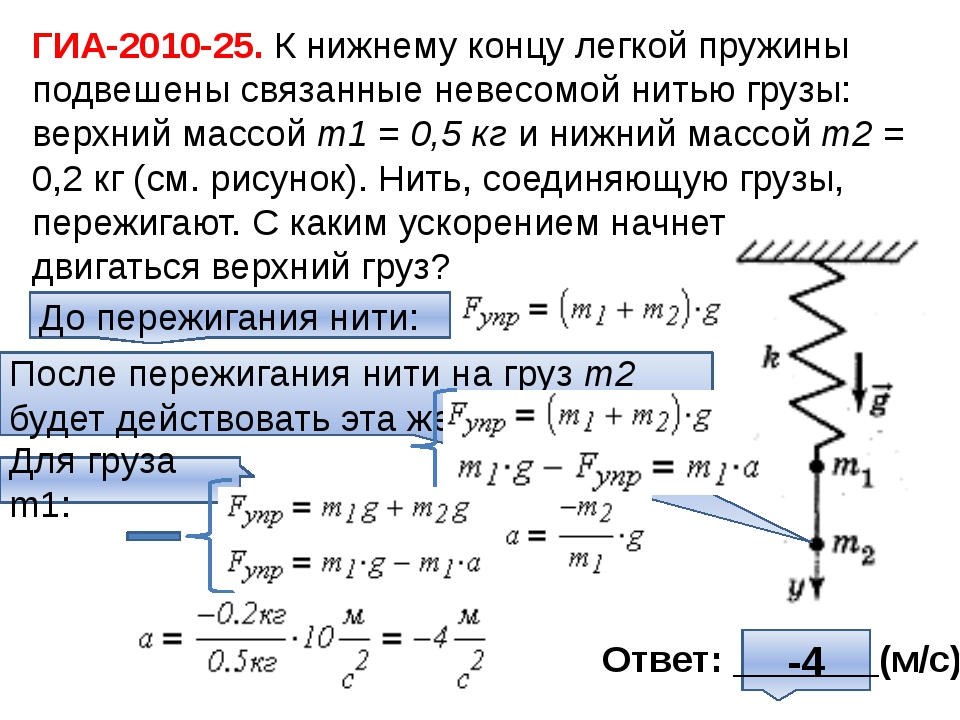 Площадь представляет собой треугольник и рассчитывается как
Площадь представляет собой треугольник и рассчитывается как
Максимальная высота складывается из трех расстояний (площадей)
Максимум. высота = 82,86 м + 195,42 м + 89,57 м = 368 мг. Когда ракета достигает точки D, время составляет 17,0 секунды. Высота на отметке 20,0 секунд составит 368 метров, поднятых над стартовой площадкой от точки A до точки D, за вычетом расстояния, упавшего с пика с 17,0 до 20,0 секунд. Это расстояние будет представлено отрицательной областью на графике скорость-время. Площадь представляет собой треугольник и может быть вычислена, если известна скорость в 20 секунд.Его можно рассчитать с помощью кинематического уравнения, а затем использовать для определения площади треугольника. В качестве альтернативы можно использовать кинематическое уравнение для определения расстояния, пройденного за эти 3,0 секунды. Работа представлена ниже:
d = v o * t + 0,5 * a * t 2 = 0,5 * (-9,8 м / с / с) * (3,0 с) 2 = 44,1 м Таким образом, высота на отметке 20 секунд равна ~ 369 м, набранной за первые 17 секунд минус ~ 44 м, упавшей в следующие 3 секунды. Ответ: 325 м .
Ответ: 325 м .
г. Ракета поднимается на 369 м за первые 17,0 секунды. За это время ракета должна упасть на 369 метров. Время падения с высоты 369 м можно определить из того же кинематического уравнения, которое использовалось в части c.
d = v o * t + 0,5 * a * t 2-368 м = 0,5 * (-9,8 м / с / с) * т 2
t = 8,67 секунды
Это время может быть добавлено к 17.0 секундам, чтобы определить время приземления ракеты: 25.7 секунд .
[# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]49. В эстафете на 200,0 м (длина каждого этапа 50,0 м) один пловец имеет преимущество на 0,450 секунды и плывет с постоянной скоростью 3,90 м / с к противоположному концу бассейна. Какая минимальная скорость должна быть у второго пловца, чтобы догнать первого к концу бассейна?
Ответ: 4,04 м / с
Оба пловца проплывают одинаковое расстояние (50 м) с постоянной скоростью. Пловец А (которого только что назвали произвольно) получает фору в 0,450 секунды. Таким образом, пловец B должен двигаться быстрее, чтобы финишировать быстрее, чем пловец A. Во-первых, можно вычислить время, необходимое пловцу A для преодоления 5010 м со скоростью 3,90 м / с. Время
Пловец А (которого только что назвали произвольно) получает фору в 0,450 секунды. Таким образом, пловец B должен двигаться быстрее, чтобы финишировать быстрее, чем пловец A. Во-первых, можно вычислить время, необходимое пловцу A для преодоления 5010 м со скоростью 3,90 м / с. Время
Таким образом, пловец В должен пройти те же 50,0 м за 12,37 секунды (12,82–0,45 с). Таким образом, скорость пловца B может быть вычислена как
. v B = d / t B = (50.0 м) / (12,37 с) = 4,04 м / с [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]50. Драг-рейсер ускоряется из состояния покоя со средней скоростью +13,2 м / с 2 на расстояние 100 м. Водитель движется по инерции в течение 0,500 секунд, а затем использует тормоза и парашют для замедления до конца трассы. Если общая длина трассы составляет 180 м, какая минимальная скорость замедления должна быть у гонщика, чтобы остановиться до конца трассы?
Ответ: -24 м / с / с
К этой проблеме можно подойти, сначала определив расстояние, на котором драгстер замедляется.Это расстояние будет меньше 80 метров на величину, равную расстоянию, которое драгстер преодолевает после пересечения финишной черты. См. Диаграмму.
Расстояние, пройденное драгстером до торможения, составляет 100 м плюс расстояние наката. Дистанцию наката можно определить, если определить скорость драгстера на конце 100 м. Итак, сначала кинематическое уравнение будет использоваться для определения скорости, а затем будет вычислено расстояние движения накатом.
Используя уравнение v f 2 = v o 2 + 2 * a * d, можно определить скорость через 100 м.Эта замена и решение показаны ниже.
v f 2 = v o 2 + 2 * a * d = 2 * (13,2 м / с / с) * (100 м) = 2640 м 2 / с 2v f = 51,4 м / с
Выбег со скоростью 51,38 м / с в течение 0,500 с приведет к пройденному расстоянию 25,7 м.
По окончании периода движения накатом остается небольшое расстояние для замедления до остановки. Это расстояние
180 м — 100 м — 25,7 м = 54 мТеперь то же кинематическое уравнение можно использовать для определения скорости замедления на последних 54 м пути.Известная информация: v o = 51,4 м / с; v f = 0 м / с; и d = 54 м. Используя уравнение v f 2 = v o 2 + 2 * a * d, можно вычислить ускорение.
a = (v f 2 — v o 2 ) / (2 * d) = = [(51,4 м / с) 2 — (0 м / с) 2 ] / ( 2 * 54 м) = -24 м / с 2 . [# 43 | # 44 | # 45 | # 46 | # 47 | # 48 | # 49 | # 50]Перейдите к:
Обзорная сессия Домашняя страница — Листинг1D Kinematics — Домашняя страница || Версия для печати || Вопросы и ссылки
Ответы на вопросы: # 1-7 || №8- №28 || # 29- # 42 || # 43- # 50
Вам тоже может понравиться…
Пользователи The Review Session часто ищут учебные ресурсы, которые предоставляют им возможности для практики и обзора, которые включают встроенную обратную связь и инструкции. Если это то, что вы ищете, то вам также может понравиться следующее:- Блокнот калькулятора
Блокнот калькулятора включает текстовые задачи по физике, сгруппированные по темам. Каждая проблема сопровождается всплывающим ответом и аудиофайлом, в котором подробно объясняется, как подойти к проблеме и решить ее.Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем.
Посещение: Панель калькулятора На главную | Подставка для калькулятора — кинематика
- Minds On Physics App Series
Minds On Physics the App («MOP the App») представляет собой серию интерактивных модулей вопросов для учащихся, которые серьезно настроены улучшить свое концептуальное понимание физики. Каждый модуль этой серии посвящен отдельной теме и разбит на подтемы.«Опыт MOP» предоставит учащемуся сложные вопросы, отзывы и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, Chromebook и компьютеров Macintosh. Это идеальный ресурс для тех, кто желает усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает в себя кинематические концепции и кинематические графики.
Посетите: MOP the App Home || MOP приложение — часть 1
Веб-сайт класса физики
Слон и перо — сопротивление воздуха
Предположим, что слон и перо одновременно падают с очень высокого здания с одной и той же высоты.Мы предположим реалистичную ситуацию, когда и перо, и слон сталкиваются с сопротивлением воздуха. Какой объект — слон или перо — упадет на землю первым? Анимация справа точно отображает эту ситуацию. Показано движение слона и пера при наличии сопротивления воздуха. Кроме того, ускорение каждого объекта представлено векторной стрелкой.
Большинство людей не удивляются тому факту, что слон ударяется о землю раньше, чем перо.Но почему слон падает быстрее? Этот вопрос является источником большой путаницы (а также множества заблуждений). Проверьте свое понимание, попытавшись определить следующие утверждения как истинные или ложные.
ИСТИНА или ЛОЖЬ:
- Слон испытывает меньшее сопротивление воздуха, чем перо, и поэтому падает быстрее.
- У слона большее ускорение свободного падения, чем у пера, и поэтому он падает быстрее.
- И у слона, и у пера одинаковая сила тяжести, но у слона наибольшее ускорение свободного падения.
- И слон, и перо имеют одинаковую силу тяжести, но перо испытывает большее сопротивление воздуха.
- Каждый объект испытывает одинаковое сопротивление воздуха, но слон испытывает наибольшую силу тяжести.
- Каждый объект испытывает одинаковое сопротивление воздуха, но перо испытывает наибольшую силу тяжести.
- Перо весит больше, чем слон, и поэтому не будет ускоряться так быстро, как слон.
- И слон, и перо весят одинаково, но большая масса пера приводит к меньшему ускорению.
- Слон испытывает меньшее сопротивление воздуха, чем перо, и поэтому достигает большей конечной скорости.
- Перо испытывает большее сопротивление воздуха, чем слон, и поэтому достигает меньшей конечной скорости.
- Слон и перо испытывают одинаковое сопротивление воздуха, но у слона конечная скорость выше.
Если вы ответили ВЕРНО на любой из вышеперечисленных вопросов, то, возможно, у вас возникла некоторая путаница в отношении понятий веса, силы тяжести, ускорения свободного падения, сопротивления воздуха и конечной скорости. Слон и перо тянут вниз под действием силы тяжести. При первоначальном падении эта сила тяжести является неуравновешенной.Таким образом, и слон, и перо начинают ускоряться (т.е. набирать скорость). Когда слон и перо начинают набирать скорость, они сталкиваются с восходящей силой сопротивления воздуха. Сопротивление воздуха является результатом того, что объект пробивает сквозь слой воздуха и сталкивается с молекулами воздуха. Чем больше молекул воздуха, с которыми сталкивается объект, тем больше сила сопротивления воздуха. Следовательно, величина сопротивления воздуха зависит от скорости падающего объекта и площади поверхности падающего объекта.Основываясь только на площади поверхности, можно с уверенностью предположить, что (при той же скорости) слон столкнется с большим сопротивлением воздуха, чем перо.
Но почему же тогда слон, который встречает большее сопротивление воздуха, чем перо, падает быстрее? В конце концов, разве сопротивление воздуха не замедляет движение объекта? Разве объект с большим сопротивлением воздуха не будет падать медленнее?
Ответ на эти вопросы требует понимания первого и второго закона Ньютона и концепции конечной скорости.Согласно законам Ньютона, объект будет ускоряться, если силы, действующие на него, неуравновешены; и, кроме того, величина ускорения прямо пропорциональна величине чистой силы (неуравновешенной силы), действующей на нее. Падающие объекты изначально ускоряются (набирают скорость), потому что нет силы, достаточно большой, чтобы уравновесить направленную вниз силу тяжести. Тем не менее, когда объект набирает скорость, он сталкивается с возрастающей силой сопротивления воздуха, направленной вверх. Фактически, объекты будут продолжать ускоряться (набирать скорость) до тех пор, пока сила сопротивления воздуха не возрастет до достаточно большого значения, чтобы уравновесить направленную вниз силу тяжести.Поскольку слон имеет большую массу, он весит больше и испытывает большую силу тяжести, направленную вниз. Слону придется ускоряться (набирать скорость) в течение более длительного периода времени, прежде чем появится достаточное сопротивление восходящего воздуха, чтобы уравновесить большую нисходящую силу тяжести.
Когда направленная вверх сила сопротивления воздуха объекту становится достаточно большой, чтобы уравновесить направленную вниз силу тяжести, считается, что объект достиг конечной скорости. Конечная скорость — это конечная скорость объекта; объект будет продолжать падать на землю с этой конечной скоростью.В случае слона и пера конечная скорость слона намного выше, чем у пера. Как упоминалось выше, слону придется ускоряться в течение более длительного периода времени. Слону требуется большая скорость, чтобы накопить достаточную силу сопротивления восходящего воздуха, чтобы уравновесить нисходящую силу тяжести. Фактически, слон никогда не достигает предельной скорости; анимация выше показывает, что в момент перед ударом о землю у слона все еще есть ускорение.Если бы мы изобразили относительную величину двух сил, действующих на слона и перо в разное время при их падении, возможно, это выглядело бы так, как показано ниже. (ПРИМЕЧАНИЕ: величина вектора силы указывается относительным размером стрелки.)
Обратите внимание на приведенные выше диаграммы и приведенную выше анимацию, что перо быстро достигает баланса сил и, следовательно, нулевого ускорения (то есть конечной скорости). С другой стороны, слон никогда не достигает предельной скорости во время падения; силы никогда не становятся полностью уравновешенными, и поэтому ускорение все еще присутствует.Если дать достаточно времени, возможно, слон наконец разгонится до достаточно высоких скоростей, чтобы столкнуться с достаточно большой силой сопротивления воздуха, направленной вверх, чтобы достичь конечной скорости. Если бы оно действительно достигло конечной скорости, то эта скорость была бы чрезвычайно большой — намного больше, чем конечная скорость пера.
Итак, в заключение, слон падает быстрее, чем перо, потому что он никогда не достигает конечной скорости; он продолжает ускоряться при падении (накапливая все большее и большее сопротивление воздуха), приближаясь к конечной скорости, но никогда не достигая ее.С другой стороны, перо быстро достигает конечной скорости. Не требуя большого сопротивления воздуха, прежде чем оно прекратит свое ускорение, перо приобретает состояние предельной скорости на ранней стадии своего падения. Малая конечная скорость пера означает, что оставшаяся часть его падения будет происходить с небольшой конечной скоростью.
Но что, если бы не было сопротивления воздуха? Если бы сопротивление воздуха можно было как-то устранить (проводя эксперимент в вакууме), то какой объект — слон или перо — первым ударил бы о землю? Изучите эти вопросы, перейдя по соответствующим ссылкам на «Слон и перо (свободное падение)» в Multimedia Physics Studios.
Для получения дополнительной информации о физических описаниях движения посетите The Physics Classroom Tutorial. Подробная информация доступна по следующим темам:
Ускорение силы тяжестиПервый закон движения Ньютона
Сила тяжести и вес
Второй закон движения Ньютона
Диаграммы свободного тела
Зависимость свободного падения от сопротивления воздуха
5.5 Третий закон Ньютона | Университетская физика, том 1,
Цели обучения
К концу раздела вы сможете:
- Третий закон движения Ньютона.
- Определите силы действия и реакции в различных ситуациях
- Применить третий закон Ньютона для определения систем и решения проблем движения
До сих пор мы рассматривали силу как толчок или тягу; однако, если вы подумаете об этом, вы поймете, что никакие толчки или тяги никогда не возникают сами по себе.Когда вы толкаете стену, она толкает вас назад. Это подводит нас к третьему закону Ньютона .
Третий закон движения Ньютона
Каждый раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает. Математически, если тело A прикладывает силу [латекс] \ overset {\ to} {F} [/ latex] к телу B , то B одновременно прикладывает силу [латекс] \ text {-} \ overset {\ to} {F} [/ latex] на A , или в форме векторного уравнения,
[латекс] {\ overset {\ to} {F}} _ {\ text {AB}} = \ text {-} {\ overset {\ to} {F}} _ {\ text {BA}}.[/ латекс]
Третий закон Ньютона представляет собой определенную симметрию в природе: силы всегда возникают парами, и одно тело не может воздействовать силой на другое, не испытав силы. Мы иногда в общих чертах называем этот закон «действие-противодействие», где приложенная сила — это действие, а сила, испытываемая как следствие, — это противодействие. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.
Мы легко можем увидеть в действии третий закон Ньютона, посмотрев на то, как люди передвигаются.Представьте себе пловца, отталкивающегося от края бассейна ((Рисунок)). Она отталкивается ногами о стену бассейна и ускоряется в направлении, противоположном ее толчку. Стена оказала на пловца равную и противоположную силу. Вы можете подумать, что две равные и противоположные силы уравновешиваются, но это не , потому что они действуют на разные системы . В этом случае мы можем исследовать две системы: пловец и стенку. Если мы выберем пловца в качестве интересующей нас системы, как на рисунке, тогда [латекс] {F} _ {\ text {wall on feet}} [/ latex] является внешней силой в этой системе и влияет на ее движение.Пловец движется в направлении этой силы. Напротив, сила [латекс] {F} _ {\ text {feet on wall}} [/ latex] действует на стену, а не на интересующую нас систему. Таким образом, [латекс] {F} _ {\ text {ноги на стене}} [/ латекс] не влияет напрямую на движение системы и не отменяет [латекс] {F} _ {\ text {стена на ногах} }. [/ latex] Пловчиха толкает в направлении, противоположном тому, в котором она хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении. В диаграмме свободного тела, такой как показанная на рисунке, мы никогда не включаем обе силы пары действие-противодействие; в этом случае мы используем только [латекс] {F} _ {\ text {стена на ногах}} [/ латекс], а не [латекс] {F} _ {\ text {ноги на стене}} [/ латекс].
Рисунок 5.16 Когда пловец воздействует на стену, она ускоряется в противоположном направлении; другими словами, чистая внешняя сила действует на нее в направлении, противоположном [латексу] {F} _ {\ text {ноги на стене}}. [/ latex] Это противодействие возникает из-за того, что в соответствии с третьим законом Ньютона стена оказывает на пловца силу [латекс] {F} _ {\ text {wall on feet}} [/ latex], равную по величине, но в направлении, противоположном тому, которое она оказывает на него. Линия вокруг пловца указывает на интересующую его систему.Таким образом, диаграмма свободного тела показывает только [латекс] {F} _ {\ text {wall on feet}}, [/ latex] w (гравитационная сила) и BF, которая является выталкивающей силой воды, поддерживающей вес пловца. Вертикальные силы w и BF компенсируются, поскольку нет вертикального ускорения.
Легко найти другие примеры третьего закона Ньютона:
- Когда профессор ходит перед доской, он прикладывает силу к полу назад. Пол оказывает на профессора противодействующую силу, которая заставляет его ускоряться.
- Автомобиль ускоряется вперед, потому что земля толкает ведущие колеса вперед в ответ на движение ведущих колес по земле. Вы можете увидеть свидетельство того, что колеса отталкиваются назад, когда колеса вращаются на гравийной дороге и отбрасывают камни назад.
- Ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большое обратное усилие на газ в камере сгорания ракеты; следовательно, газ оказывает на ракету большую реактивную силу.Эта сила реакции, которая толкает тело вперед в ответ на силу, направленную назад, называется толчком и . Распространенное заблуждение, что ракеты движутся сами по себе, толкаясь о землю или воздух позади них. На самом деле они лучше работают в вакууме, где им легче выводить выхлопные газы.
- Вертолеты создают подъемную силу, выталкивая воздух вниз, тем самым испытывая восходящую силу реакции.
- Птицы и самолеты также летают, воздействуя на воздух силой в направлении, противоположном той силе, которая им нужна.Например, крылья птицы заставляют воздух двигаться вниз и назад, чтобы подняться и двигаться вперед.
- Осьминог движется в воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу.
- Когда человек тянет вниз по вертикальной веревке, веревка тянет человека вверх ((Рисунок)).
Рисунок 5.17 Когда альпинист тянет вниз веревку, веревка тянет вверх альпиниста.
Есть две важные особенности третьего закона Ньютона.Во-первых, прилагаемые силы (действие и противодействие) всегда равны по величине, но противоположны по направлению. Во-вторых, эти силы действуют на разные тела или системы: сила A действует на B , а сила B действует на A . Другими словами, две силы — это разные силы, которые не действуют на одно и то же тело. Таким образом, они не отменяют друг друга.
Для ситуации, показанной на (Рисунок), третий закон указывает, что, поскольку стул толкает мальчика вверх с силой [латекс] \ overset {\ to} {C}, [/ латекс] он толкает стул вниз. с силой [латекс] \ text {-} \ overset {\ to} {C}.[/ latex] Точно так же он толкает вниз с силами [latex] \ text {-} \ overset {\ to} {F} [/ latex] и [latex] \ text {-} \ overset {\ to} {T } [/ latex] на полу и на столе соответственно. Наконец, поскольку Земля тянет мальчика вниз с силой [латекс] \ overset {\ to} {w}, [/ latex], он тянет вверх на Земле с силой [латекс] \ text {-} \ overset {\ to} { ш} [/ латекс]. Если бы этот студент в отчаянии сердито ударил по столу, он быстро усвоил бы болезненный урок (которого можно избежать, изучая законы Ньютона), что стол наносит столь же сильный удар.
Человек, идущий или бегущий, инстинктивно применяет третий закон Ньютона. Например, бегун на (Рис.) Толкает назад землю так, что это толкает его вперед.
Рисунок 5.18 Бегун подчиняется третьему закону Ньютона. (а) Бегун прилагает силу к земле. (b) Сила реакции земли на бегуна толкает его вперед.
Пример
Силы на стационарном объекте
Пакет на (Рис.) Стоит на весах.Силы, действующие на упаковку, следующие: [латекс] \ overset {\ to} {S}, [/ latex], что связано с масштабом, и [латекс] \ text {-} \ overset {\ to} {w}, [ / latex], который возникает из-за гравитационного поля Земли. Силы реакции, которые оказывает упаковка, следующие: [latex] \ text {-} \ overset {\ to} {S} [/ latex] на шкале и [latex] \ overset {\ to} {w} [/ latex] на Земля. Поскольку пакет не ускоряется, применение второго закона дает
[латекс] \ overset {\ to} {S} — \ overset {\ to} {w} = m \ overset {\ to} {a} = \ overset {\ to} {0}, [/ latex]
т.
[латекс] \ overset {\ to} {S} = \ overset {\ to} {w}.[/ латекс]
Таким образом, показания весов показывают величину веса упаковки. Однако весы не измеряют вес упаковки; он измеряет силу [латекс] \ text {-} \ overset {\ to} {S} [/ latex] на своей поверхности. Если система ускоряется, [latex] \ overset {\ to} {S} [/ latex] и [latex] \ text {-} \ overset {\ to} {w} [/ latex] не будут равны, поскольку объяснено в Приложениях законов Ньютона.
Рис. 5.19 (a) Силы, действующие на упаковку, лежащую на весах, вместе с их силами реакции.Сила [латекс] \ overset {\ to} {w} [/ latex] — это вес упаковки (сила, вызванная гравитацией Земли), а [латекс] \ overset {\ to} {S} [/ latex] — это сила весов на упаковке. (b) Изоляция системы «пакет-масштаб» и системы «пакет-Земля» делает ясными пары действия и реакции.
Пример
Начало работы: выбор правильной системы
Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал ((Рисунок)).Ее масса 65,0 кг, масса тележки 12,0 кг, масса оборудования 7,0 кг. Вычислите ускорение, возникающее, когда профессор прикладывает к полу силу 150 Н. Все силы, противодействующие движению, такие как трение колес тележки и сопротивление воздуха, составляют 24,0 Н.
Рисунок 5.20 Профессор толкает тележку со своим демонстрационным оборудованием. Длины стрелок пропорциональны величине сил (кроме [latex] \ overset {\ to} {f} \ text {,} [/ latex], потому что они слишком малы для масштабирования).Система 1 подходит для этого примера, потому что она запрашивает ускорение всей группы объектов. Только [латекс] {\ overset {\ to} {F}} _ {\ text {floor}} [/ latex] и [latex] \ overset {\ to} {f} [/ latex] являются внешними силами, действующими на систему 1 по линии движения. Все остальные силы либо отменяют, либо действуют во внешнем мире. Система 2 выбрана для следующего примера, так что [latex] {\ overset {\ to} {F}} _ {\ text {prof}} [/ latex] является внешней силой и входит во второй закон Ньютона. Диаграммы свободного тела, которые служат основой второго закона Ньютона, меняются в зависимости от выбранной системы.
Стратегия
Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это Система 1 на (Рисунок). Профессор толкает назад с силой [латекс] {F} _ {\ text {foot}} [/ latex] в 150 Н. Согласно третьему закону Ньютона, пол создает силу реакции вперед [латекс] {F} _ { \ text {floor}} [/ latex] 150 Н в Системе 1. Поскольку все движения горизонтальны, мы можем предположить, что в вертикальном направлении нет результирующей силы. Следовательно, задача одномерная по горизонтали.Как уже отмечалось, трение f противодействует движению и, таким образом, имеет направление, противоположное [латексному] {F} _ {\ text {floor}}. [/ latex] Мы не включаем силы [латекс] {F} _ {\ text {prof}} [/ latex] или [latex] {F} _ {\ text {cart}} [/ latex], потому что они внутренние силы, и мы не включаем [латекс] {F} _ {\ text {foot}} [/ latex], потому что он действует на пол, а не на систему. Никаких других значительных сил, действующих на Систему 1. Если чистая внешняя сила может быть найдена из всей этой информации, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение.См. Диаграмму свободного тела на рисунке.
Решение
Второй закон Ньютона дает
[латекс] a = \ frac {{F} _ {\ text {net}}} {m}. [/ латекс]
Чистая внешняя сила, действующая на Систему 1, выводится из (Рисунок) и предыдущего обсуждения, чтобы быть
.[латекс] {F} _ {\ text {net}} = {F} _ {\ text {floor}} — f = 150 \, \ text {N} -24.0 \, \ text {N} = 126 \ , \ text {N} \ text {.} [/ latex]
Масса Системы 1
[латекс] m = (65,0 + 12,0 + 7,0) \, \ text {кг} = 84 \, \ text {кг} \ text {.{2}. [/ латекс]
Значение
Ни одна из сил между компонентами Системы 1, например, между руками профессора и тележкой, не влияет на чистую внешнюю силу, потому что они являются внутренними по отношению к Системе 1. Другой способ взглянуть на это состоит в том, что силы между компонентами системы отменяются. потому что они равны по величине и противоположны по направлению. Например, сила, прилагаемая профессором к тележке, приводит к тому, что на профессора действует равная и противоположная сила. В этом случае обе силы действуют на одну и ту же систему и, следовательно, отменяются.Таким образом, внутренние силы (между компонентами системы) отменяются. Выбор Системы 1 имел решающее значение для решения этой проблемы.
Пример
Усилие на тележке: выбор новой системы
Рассчитайте силу, которую профессор оказывает на тележку (рисунок), используя при необходимости данные из предыдущего примера.
Стратегия
Если мы определим интересующую систему как тележку плюс оборудование (Система 2 на (Рисунок)), то чистая внешняя сила в Системе 2 — это сила, которую профессор оказывает на тележку за вычетом трения.Сила, которую она оказывает на тележку, [латекс] {F} _ {\ text {prof}} [/ latex], является внешней силой, действующей на Систему 2. [latex] {F} _ {\ text {prof}} [/ latex] был внутренним по отношению к Системе 1, но он был внешним по отношению к Системе 2 и, таким образом, входит во второй закон Ньютона для этой системы.
Решение
Второй закон Ньютона можно использовать для поиска [латекса] {F} _ {\ text {prof}}. [/ latex] Начнем с
[латекс] a = \ frac {{F} _ {\ text {net}}} {m}. [/ латекс]
Величина чистой внешней силы в Системе 2 составляет
.[латекс] {F} _ {\ text {net}} = {F} _ {\ text {prof}} — ф.[/ латекс]
Решаем за [латекс] {F} _ {\ text {prof}} [/ latex], желаемое количество:
[латекс] {F} _ {\ text {prof}} = {F} _ {\ text {net}} + f. [/ латекс]
Дано значение f , поэтому мы должны вычислить net [latex] {F} _ {\ text {net}}. [/ latex] Это можно сделать, потому что известны и ускорение, и масса Системы 2. Используя второй закон Ньютона, мы видим, что
[латекс] {F} _ {\ text {net}} = ma, [/ latex]
, где масса Системы 2 равна 19.{2}) = 29 \, \ text {N} \ text {.} [/ Latex]
Теперь мы можем найти желаемую силу:
[латекс] {F} _ {\ text {prof}} = {F} _ {\ text {net}} + f = 29 \, \ text {N} +24.0 \, \ text {N} = 53 \ , \ text {N} \ text {.} [/ latex]
Значение
Эта сила значительно меньше, чем сила в 150 Н, которую профессор приложил к полу. Не вся сила 150 Н передается на тележку; кое-что ускоряет профессора. Выбор системы — важный аналитический шаг как в решении проблем, так и в глубоком понимании физики ситуации (что не обязательно одно и то же).
Проверьте свое понимание
Два блока находятся в покое и контактируют на поверхности без трения, как показано ниже, с [latex] {m} _ {1} = 2.0 \, \ text {kg}, [/ latex] [latex] {m} _ { 2} = 6.0 \, \ text {kg}, [/ latex] и приложенная сила 24 Н. (a) Найдите ускорение системы блоков. (b) Предположим, что блоки позже разделятся. Какая сила даст второму блоку массой 6,0 кг такое же ускорение, как и система блоков?
Показать решениеа.{2} [/ латекс]; б. 18 N
Сводка
- Третий закон движения Ньютона представляет собой основную симметрию в природе, с испытываемой силой, равной по величине и противоположной по направлению действующей силе.
- Две равные и противоположные силы не отменяются, потому что они действуют на разные системы.
- Пары действие-реакция включают пловца, отталкивающего стену, вертолеты, создающие подъемную силу, выталкивая воздух вниз, и осьминога, толкающего себя вперед, выбрасывая воду из своего тела.Ракеты, самолеты и автомобили толкаются вперед за счет силы реакции тяги.
- Выбор системы — важный аналитический шаг в понимании физики проблемы и ее решении.
Концептуальные вопросы
Определите силы действия и противодействия в следующих ситуациях: (а) Земля притягивает Луну, (б) мальчик бьет футбольный мяч, (в) ракета ускоряется вверх, (г) машина ускоряется вперед, (д) высоко прыгун прыгает, и (е) из ружья выпускается пуля.
Показать решениеа. действие: Земля притягивает Луну, реакция: Луна притягивает Землю; б. действие: ступня прикладывает силу к мячу, реакция: мяч прикладывает силу к ступне; c. действие: ракета толкает газ, реакция: газ толкает ракету обратно; d. действие: автомобильные шины толкают назад по дороге, реакция: дорога толкает вперед шины; е. действие: парашютист толкает перемычку вниз, реакция: земля толкает перемычку; f. Действие: пистолет толкает пулю вперед, реакция: пуля толкает пистолет назад.
Предположим, вы держите в руке чашку кофе.Определите все силы на чашке и реакцию на каждую силу.
(a) Почему обычная винтовка дает отдачу (отдачу назад) при выстреле? (b) Ствол безоткатного ружья открыт с обоих концов. Опишите, как действует третий закон Ньютона при увольнении. (c) Можете ли вы безопасно стоять рядом с одним из них, когда из него стреляют?
Показать решениеа. Винтовка (снаряд, поддерживаемый винтовкой) прикладывает силу, чтобы выбить пулю; реакция на эту силу — это сила, которую пуля оказывает на винтовку (снаряд) в противоположном направлении.{2} [/ латекс]. (а) Какова сила трения между ногами проигравшего игрока и травой? (b) Какую силу прилагает выигравший игрок к земле, чтобы двигаться вперед, если его масса плюс снаряжение составляет 110,0 кг?
Книга по истории лежит на столе по физике, как показано ниже; также показана диаграмма свободного тела. Книги по истории и физике весят 14 Н и 18 Н соответственно. Обозначьте каждую силу, действующую на каждую книгу, с помощью двойного нижнего индекса (например, сила контакта книги истории, прижатой к книге физики, может быть описана как [латекс] {\ overset {\ to} {F}} _ {\ text {HP }} [/ latex]) и определите значение каждой из этих сил, объясняя используемый процесс.
Показать решениеПоскольку вес книги по истории — это сила, прилагаемая Землей к книге по истории, мы представляем ее как [латекс] {\ overset {\ to} {F}} _ {\ text {EH}} = — 14 \ hat {j} \, \ text {N} \ text {.} [/ latex] Помимо этого, книга истории взаимодействует только с книгой физики. Поскольку ускорение книги истории равно нулю, чистая сила, действующая на нее, равна нулю по второму закону Ньютона: [латекс] {\ overset {\ to} {F}} _ {\ text {PH}} + {\ overset {\ to} {F}} _ {\ text {EH}} = \ overset {\ to} {0}, [/ latex] где [latex] {\ overset {\ to} {F}} _ {\ text {PH }} [/ latex] — это сила, прилагаемая книгой по физике к учебнику истории.Таким образом, [латекс] {\ overset {\ to} {F}} _ {\ text {PH}} = \ text {-} {\ overset {\ to} {F}} _ {\ text {EH}} = \ text {-} (- 14 \ hat {j}) \, \ text {N} = 14 \ hat {j} \, \ text {N} \ text {.} [/ latex] Мы обнаруживаем, что книга по физике оказывает на книгу истории восходящую силу величиной 14 Н. На книгу по физике действуют три силы: [латекс] {\ overset {\ to} {F}} _ {\ text {EP}} [/ latex] из-за Земли, [латекс] {\ overset {\ to} {F}} _ {\ text {HP}} [/ latex] из-за книги по истории и [latex] {\ overset {\ to} {F}} _ {\ text {DP}} [/ latex] из-за на рабочий стол.Поскольку книга по физике весит 18 Н, [латекс] {\ overset {\ to} {F}} _ {\ text {EP}} = — 18 \ hat {j} \, \ text {N} \ text {.} [/ latex] Согласно третьему закону Ньютона, [latex] {\ overset {\ to} {F}} _ {\ text {HP}} = \ text {-} {\ overset {\ to} {F}} _ { \ text {PH}}, [/ latex] так [латекс] {\ overset {\ to} {F}} _ {\ text {HP}} = — 14 \ hat {j} \, \ text {N} \ text {.} [/ latex] Второй закон Ньютона, примененный к книге по физике, дает [latex] \ sum \ overset {\ to} {F} = \ overset {\ to} {0}, [/ latex] или [latex] {\ overset {\ to} {F}} _ {\ text {DP}} + {\ overset {\ to} {F}} _ {\ text {EP}} + {\ overset {\ to} {F} } _ {\ text {HP}} = \ overset {\ to} {0}, [/ latex] так [латекс] {\ overset {\ to} {F}} _ {\ text {DP}} = \ text {-} (- 18 \ hat {j}) — (- 14 \ hat {j}) = 32 \ hat {j} \, \ text {N} \ text {.{2} [/ латекс]. Найдите величину ускорения автомобиля.
Глоссарий
- Третий закон движения Ньютона
- всякий раз, когда одно тело оказывает силу на второе тело, первое тело испытывает силу, равную по величине и противоположную по направлению силе, которую оно оказывает
- тяга
- сила реакции, которая толкает тело вперед в ответ на силу противодействия
6.3 Центростремительная сила — Университетская физика, том 1
Цели обучения
К концу раздела вы сможете:
- Объясните уравнение центростремительного ускорения
- Примените второй закон Ньютона, чтобы получить уравнение для центростремительной силы
- Используйте концепции кругового движения при решении задач, связанных с законами движения Ньютона
«В движении в двух и трех измерениях» мы изучили основные концепции кругового движения.Объект, совершающий круговое движение, например один из гоночных автомобилей, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это центрально направленное ускорение, называемое центростремительным ускорением , выражается формулой
, где v — скорость объекта, направленная по касательной к кривой в любой момент времени. Если мы знаем угловую скорость
, тогда мы можем использовать
Угловая скорость — это скорость, с которой объект поворачивает по кривой, в рад / с.Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.
Ускорение должно производиться силой. Любая сила или комбинация сил могут вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение троса на тросовом шаре, сила притяжения Земли на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы, действующие на трубу вращающейся центрифуги. . Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой .Направление центростремительной силы — к центру кривизны, то же самое, что и направление центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила равна массе, умноженной на ускорение:
Для равномерного кругового движения ускорением является центростремительное ускорение: .
Таким образом, величина центростремительной силы
это
Подставляя выражения для центростремительного ускорения
получаем два выражения для центростремительной силы
по массе, скорости, угловой скорости и радиусу кривизны:
Вы можете использовать любое более удобное выражение для центростремительной силы.Центростремительная сила
всегда перпендикулярно траектории и указывает на центр кривизны, потому что
перпендикулярно скорости и указывает на центр кривизны. Обратите внимание, что если вы решите первое выражение для r , вы получите
Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть резкую кривую, как на (Рисунок).
Рисунок 6.20 Сила трения обеспечивает центростремительную силу и численно равна ей. Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше, тем меньше радиус кривизны r и круче кривизна. Вторая кривая имеет то же v, но большее значение
.дает меньшее r ‘.
Пример
Какой коэффициент трения нужен автомобилям на плоской кривой?
(a) Рассчитайте центростремительную силу, действующую на 900.Автомобиль массой 0 кг, который преодолевает поворот радиусом 500,0 м со скоростью 25,00 м / с. (b) Предполагая, что кривая без кренована, найдите минимальный статический коэффициент трения между шинами и дорогой, при этом статическое трение является причиной, препятствующей скольжению автомобиля ((Рисунок)).
Рисунок 6.21 Этот автомобиль на ровной поверхности движется в сторону и поворачивает налево. Центростремительная сила, заставляющая автомобиль вращаться по круговой траектории, возникает из-за трения между шинами и дорогой. Требуется минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и съезжать с проезжей части.Стратегия
- Мы знаем, что
Таким образом,
- (Рисунок) показывает силы, действующие на автомобиль на кривой без кренов (ровной поверхности). Трение направлено влево, предотвращая скольжение автомобиля, и поскольку это единственная горизонтальная сила, действующая на автомобиль, трение в данном случае является центростремительной силой. Мы знаем, что максимальное статическое трение (при котором шины катятся, но не скользят) составляет
где
— статический коэффициент трения, а Н, — нормальная сила.Нормальная сила равна массе автомобиля на ровной поверхности, поэтому
Таким образом, центростремительная сила в данной ситуации равна
.Теперь у нас есть связь между центростремительной силой и коэффициентом трения. Используя уравнение
получаем
Решаем это для
, отмечая, что масса отменяется, и получаем
Замена известных,
(Поскольку коэффициенты трения являются приблизительными, ответ дается только двумя цифрами.)
Значение
Коэффициент трения, указанный на (Рисунок) (b), намного меньше, чем обычно наблюдается между шинами и дорогой. Автомобиль по-прежнему движется по кривой, если коэффициент больше 0,13, потому что трение покоя является реактивной силой, которая может принимать значение меньше, но не больше
.Более высокий коэффициент также позволит автомобилю преодолевать поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет меньше 25 м / с.Обратите внимание, что масса отменяется, подразумевая, что в этом примере не имеет значения, насколько сильно загружена машина для прохождения поворота. Масса сокращается, потому что трение считается пропорциональным нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.
Проверьте свое понимание
Автомобиль, движущийся со скоростью 96,8 км / ч, движется по круговой кривой радиусом 182,9 м по ровной проселочной дороге. Какой должен быть минимальный коэффициент статического трения, чтобы автомобиль не скользил?
[показать-ответ q = ”694795 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 694795 ″] 0.40 [/ hidden-answer]
Кривые с наклоном
Давайте теперь рассмотрим кривых с наклоном , где наклон дороги помогает вам преодолевать кривую ((рисунок)). Чем больше угол
, тем быстрее вы сможете пройти кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. На «кривой с идеальным наклоном» угол
такова, что вы можете преодолевать поворот на определенной скорости без трения между шинами и дорогой.Получим выражение для
для кривой с идеальным наклоном и рассмотрим связанный с ней пример.
Рисунок 6.22 Автомобиль на этой кривой с наклоном удаляется и поворачивает налево.Для perfect bank чистая внешняя сила равна горизонтальной центростремительной силе в отсутствие трения. Составляющие нормальной силы Н, в горизонтальном и вертикальном направлениях должны равняться центростремительной силе и массе автомобиля соответственно.В случаях, когда силы не параллельны, удобнее всего рассматривать компоненты вдоль перпендикулярных осей — в данном случае вертикального и горизонтального направлений.
(рисунок) показывает диаграмму свободного тела для автомобиля на кривой без трения с наклоном. Если угол
идеально подходит для скорости и радиуса, тогда чистая внешняя сила равна необходимой центростремительной силе. Единственные две внешние силы, действующие на автомобиль, — это его вес
кг.и нормальная сила дороги
(Поверхность без трения может оказывать только силу, перпендикулярную поверхности, то есть нормальную силу.Эти две силы должны складываться, чтобы получить чистую внешнюю силу, горизонтальную по направлению к центру кривизны и имеющую величину
.Поскольку это решающая сила и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть
.Поскольку автомобиль не выезжает за пределы дороги, чистая вертикальная сила должна быть равна нулю, что означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны по направлению.Из (Рисунок) мы видим, что вертикальная составляющая нормальной силы равна
., а единственная другая вертикальная сила — это вес автомобиля. Они должны быть равны по величине; таким образом,
Теперь мы можем объединить эти два уравнения, чтобы исключить N и получить выражение для
., по желанию. Решение второго уравнения относительно
и подставив его в первое, получим
Взяв арктангенс, получаем
Это выражение можно понять, рассмотрев, как
зависит от v и r .Большой
получается для большого v и маленького r. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам двигаться по кривой с большей или меньшей скоростью, чем если бы по кривой не было трения. Обратите внимание, что
не зависит от массы автомобиля.
Пример
Какая идеальная скорость для выхода на крутой крутой поворот?
Кривые на некоторых испытательных треках и гоночных трассах, таких как Международная гоночная трасса Дейтона во Флориде, имеют очень крутой наклон.Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет преодолевать повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, при которой кривая радиусом 100,0 м переходит в
Нанужно ездить, если дорога была без трения.
Стратегия
Прежде всего отметим, что все члены в выражении для идеального угла кривой с наклоном, кроме скорости, известны; таким образом, нам нужно только переставить его так, чтобы скорость появлялась в левой части, а затем подставить известные величины.
Решение
Начиная с
получаем
Отметив, что
получаем
Значение
Это примерно 165 км / ч, что соответствует очень крутому и довольно крутому повороту. Трение шин позволяет автомобилю двигаться по кривой на значительно более высоких скоростях.
Самолеты также совершают развороты по крену. Подъемная сила, создаваемая силой воздуха, воздействующего на крыло, действует под прямым углом к крылу.Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет самолет. Угол крена, показанный на (Рисунок), равен
.. Мы анализируем силы так же, как и в случае поворота автомобиля по кривой.
Рис. 6.23 При повороте крена горизонтальная составляющая подъемной силы неуравновешивается и ускоряет самолет.Обычный компонент подъемной силы уравновешивает вес самолета. Угол крена определяется выражением. Сравните векторную диаграмму с диаграммой, показанной на (Рисунок).
Силы инерции и неинерциальные (ускоренные) рамки: сила Кориолиса
Что общего между взлетом на реактивном самолете, поворотом на автомобиле, каруселью и круговым движением тропического циклона? Каждый из них проявляет силы инерции — силы, которые кажутся просто возникающими в результате движения, потому что система отсчета наблюдателя ускоряется или вращается.При взлете на реактивном самолете большинство людей согласятся, что создается ощущение, будто вас толкают обратно в кресло, когда самолет ускоряется по взлетно-посадочной полосе. Однако физик сказал бы, что вы, , склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт происходит, когда вы делаете крутой поворот на своей машине, скажем, вправо ((рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно машины. Опять же, физик сказал бы, что вы, , движетесь по прямой (вспомните первый закон Ньютона), но автомобиль движется вправо, а не то, что вы испытываете силу слева.
Рис. 6.24 (a) Водитель автомобиля чувствует себя вынужденным влево по отношению к автомобилю при повороте направо. Это инерционная сила, возникающая в результате использования автомобиля в качестве системы отсчета. (б) В земной системе координат водитель движется по прямой, подчиняясь первому закону Ньютона, и машина движется вправо. Слева от водителя относительно Земли нет силы. Вместо этого справа на машине есть сила, заставляющая ее повернуть.Мы можем согласовать эти точки зрения, исследуя используемые системы координат.Давайте сконцентрируемся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве ориентира, в то время как физик может использовать Землю. Физик мог бы сделать этот выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в Законах Ньютона. Автомобиль представляет собой неинерциальную систему отсчета , потому что он ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, — это сила инерции , не имеющая физического происхождения (она возникает исключительно из-за инерции пассажира, а не из-за какой-либо физической причины, такой как напряжение, трение или гравитация).Автомобиль, как и водитель, действительно ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.
Физик выберет ту систему отсчета, которая наиболее удобна для анализируемой ситуации. Для физика нетрудно включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерционные (ускоренные) системы отсчета используются, когда это полезно.При обсуждении движения космонавта в космическом корабле, движущемся со скоростью, близкой к скорости света, необходимо учитывать различные системы отсчета, что вы поймете при изучении специальной теории относительности.
Давайте теперь мысленно прокатимся на карусели, а именно на быстро вращающейся игровой площадке ((Рисунок)). Вы берете карусель в качестве системы отсчета, потому что вы вращаетесь вместе. Вращаясь в этой неинерциальной системе отсчета, вы чувствуете инерционную силу, которая имеет тенденцию сбивать вас с толку; это часто называют центробежной силой (не путать с центростремительной силой).Центробежная сила — это широко используемый термин, но на самом деле его не существует. Вы должны держаться крепче, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В системе отсчета Земли нет силы, пытающейся сбить вас с толку; мы подчеркиваем, что центробежная сила — это фикция. Вы должны держаться, чтобы заставить себя двигаться по кругу, потому что в противном случае вы бы пошли по прямой, прямо с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.
Рис. 6.25 (a) Всадник на карусели чувствует себя так, как будто его сбивают с толку. Эту инерционную силу иногда ошибочно называют центробежной силой, пытаясь объяснить движение всадника во вращающейся системе отсчета. (б) В инерциальной системе отсчета и согласно законам Ньютона его уносит инерция (незатененный всадник имеети голов по прямой). Сила,
, необходим для создания кругового пути.
Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах ((Рисунок)). Центрифуга вращает образец очень быстро, как упоминалось ранее в этой главе. Если смотреть из вращающейся системы координат, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц переносит их по касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.
Рис. 6.26. Центрифуги выполняют свою задачу по инерции. Частицы в жидком осадке оседают, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет осаждение. В конечном итоге частицы соприкасаются со стенками пробирки, которые затем создают центростремительную силу, необходимую для их движения по кругу постоянного радиуса.Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета.Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на (Рисунок)? Мяч движется по прямой траектории относительно Земли (при незначительном трении) и по изогнутой вправо траектории на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а под ним вращается карусель. В системе отсчета карусели мы объясняем кажущуюся кривую справа с помощью силы инерции, называемой силой Кориолиса , которая заставляет мяч изгибаться вправо.Сила Кориолиса может использоваться кем угодно в этой системе отсчета, чтобы объяснить, почему объекты следуют изогнутыми путями, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.
Рис. 6.27. Посмотрев вниз на вращение карусели против часовой стрелки, мы видим, что шар, скользящий прямо к краю, следует по изогнутой вправо траектории. Человек перемещает мяч к точке B, начиная с точки A. Обе точки поворачиваются в затемненные положения (A ‘и B’), показанные в то время, когда мяч следует изогнутой траектории во вращающейся рамке и прямой траектории в системе координат Земли .До сих пор мы рассматривали Землю как инерциальную систему отсчета, почти не беспокоясь о эффектах, связанных с ее вращением. Однако такие эффекты и существуют — например, во вращении погодных систем. Большинство последствий вращения Земли качественно можно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на (рисунок). Как и на карусели, любое движение в Северном полушарии Земли испытывает силу Кориолиса вправо.Прямо противоположное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли мала, силой Кориолиса обычно можно пренебречь, но для крупномасштабных движений, таких как характер ветра, она оказывает существенное влияние.
Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке. (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, которые представляют собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями.) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет в любую область низкого давления, а тропические циклоны имеют особенно низкое давление. Таким образом, ветры движутся к центру тропического циклона или погодной системы низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с поднимающимся воздухом, который также вызывает охлаждение и образование облаков, что делает картины низкого давления вполне заметными из космоса.И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но менее заметна, потому что высокое давление связано с опусканием воздуха, обеспечивающим чистое небо.
Рис. 6.28 (a) Вращение этого урагана в Северном полушарии против часовой стрелки является главным следствием силы Кориолиса. (б) Без силы Кориолиса воздух поступал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветер вправо, производя вращение против часовой стрелки.(d) Ветер, выходящий из зоны высокого давления, также отклоняется вправо, вызывая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит А и кредит е: модификации работы НАСА)Вращение тропических циклонов и траектория шара на карусели также могут быть объяснены инерцией и вращением системы под ним. Когда используются неинерциальные системы отсчета, для объяснения искривленной траектории должны быть изобретены силы инерции, такие как сила Кориолиса.Физического источника этих сил инерции нет. В инерциальной системе отсчета инерция объясняет путь, и не обнаруживается сила без идентифицируемого источника. Любая точка зрения позволяет нам описывать природу, но взгляд в инерциальной системе отсчета является самым простым в том смысле, что все силы имеют истоки и объяснения.
Концептуальные вопросы
Если вы хотите уменьшить нагрузку (которая связана с центростремительной силой) на высокоскоростные шины, вы бы использовали шины большого или малого диаметра? Объяснять.
Определите центростремительную силу. Может ли сила любого типа (например, натяжение, сила тяжести, трение и т. Д.) Быть центростремительной силой? Может ли любое сочетание сил быть центростремительной силой?
[показывать-ответ q = ”fs-id1165039453744 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165039453744 ″]
Центростремительная сила определяется как любая чистая сила, вызывающая равномерное круговое движение. Центростремительная сила — это не новый вид силы. Обозначение «центростремительная» относится к любой силе , которая заставляет что-то вращаться по кругу.Эта сила может быть напряжением, гравитацией, трением, электрическим притяжением, нормальной силой или любой другой силой. Любая их комбинация может быть источником центростремительной силы, например, центростремительная сила в верхней части траектории троса, проходящего через вертикальный круг, является результатом как напряжения, так и силы тяжести.
[/ hidden-answer]
Если центростремительная сила направлена к центру, почему вы чувствуете, что вас «отбрасывает» от центра, когда машина движется по кривой? Объяснять.
Водители гоночных автомобилей обычно срезают углы, как показано ниже (Путь 2). Объясните, как это позволяет снимать кривую с максимальной скоростью.
[раскрыть-ответ q = «329939 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =» 329939 ″] Водитель, который срезает угол (на Пути 2), имеет более плавную кривую с большей радиус. Это будет лучшая гоночная трасса. Если водитель слишком быстро завернет за угол, используя гоночную трассу, он все равно соскользнет с трассы; главное — поддерживать максимальное значение статического трения.Итак, водитель хочет максимально возможной скорости и максимального трения. Рассмотрим уравнение для центростремительной силы:
где v — скорость, а r — радиус кривизны. Таким образом, уменьшая кривизну (1 / r) пути, по которому движется автомобиль, мы уменьшаем силу, которую шины должны оказывать на дорогу, что означает, что теперь мы можем увеличить скорость v. вид водителя на Пути 1, мы можем рассуждать так: чем круче поворот, тем меньше радиус поворота; чем меньше диаметр поворота, тем больше требуется центростремительная сила.Если эта центростремительная сила не приложена, результатом будет занос. [/ Hidden-answer]
Во многих парках развлечений есть аттракционы с вертикальными петлями, как показано ниже. В целях безопасности автомобили прикреплены к рельсам таким образом, чтобы они не могли упасть. Если автомобиль преодолевает вершину с правильной скоростью, только сила тяжести будет обеспечивать центростремительную силу. Какая еще сила действует и в каком направлении, если:
(a) Автомобиль преодолевает вершину быстрее этой скорости?
(b) Автомобиль переезжает через вершину со скоростью ниже этой?
Что заставляет воду удаляться с одежды в центрифуге?
[показывать-ответ q = ”fs-id1165039477270 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165039477270 ″]
Цилиндр сушилки создает центростремительную силу на одежде (включая капли воды), заставляя ее двигаться по круговой траектории.Когда капля воды попадает в одно из отверстий бочки, она перемещается по касательной к окружности.
[/ hidden-answer]
Когда фигурист образует круг, какая сила отвечает за его поворот? Используйте в своем ответе диаграмму свободного тела.
Предположим, что ребенок едет на карусели примерно на полпути между ее центром и краем. У нее есть коробка для завтрака, покоящаяся на вощеной бумаге, так что между ней и каруселью очень мало трения.По какому пути, показанному ниже, пойдет коробка с обедом, когда она отпустит? Ланч-бокс оставляет след в пыли на карусели. Эта тропа прямая, изогнута влево или вправо? Поясните свой ответ.
[раскрыть-ответ q = ”60053 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 60053 ″] Если нет трения, значит и центростремительной силы нет. Это означает, что коробка для завтрака будет двигаться по касательной к кругу и, таким образом, следует по пути B. След пыли будет прямым.Это результат первого закона движения Ньютона. [/ Hidden-answer]
Чувствуете ли вы, что вас бросает в любую сторону, когда вы проезжаете поворот, который идеально соответствует скорости вашего автомобиля? В каком направлении на вас действует сила автокресла?
Предположим, что масса движется по круговой траектории на столе без трения, как показано ниже. В земной системе отсчета нет центробежной силы, оттягивающей массу от центра вращения, но есть сила, растягивающая нить, прикрепляющую массу к гвоздю.Используя концепции, связанные с центростремительной силой и третьим законом Ньютона, объясните, какая сила натягивает струну, указав ее физическое происхождение.
[показать-ответ q = ”965193 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 965193 ″] Для поддержания кругового движения должна быть центростремительная сила; это обеспечивается гвоздем в центре. Третий закон Ньютона объясняет это явление. Сила воздействия — это сила струны, действующая на массу; сила реакции — это сила массы, действующая на струну.Эта сила реакции заставляет струну растягиваться. [/ Hidden-answer]
Когда смывается унитаз или сливается раковина, вода (и другие материалы) по пути вниз начинает вращаться вокруг слива. Предполагая, что начального вращения нет и поток изначально направлен прямо к водостоку, объясните, что вызывает вращение и какое направление оно имеет в Северном полушарии. (Обратите внимание, что это небольшой эффект, и в большинстве туалетов вращение вызывается направленными водяными струями.) Будет ли направление вращения измениться на противоположное, если вода будет вытесняться в канализацию?
Автомобиль объезжает поворот и наталкивается на кусок льда с очень низким коэффициентом кинетической фиксации.Автомобиль съезжает с дороги. Опишите путь, по которому машина съезжает с дороги.
[показывать-ответ q = ”fs-id116503
62 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id116503
62 ″]
Поскольку радиальное трение с шинами обеспечивает центростремительную силу, а трение почти равно нулю, когда автомобиль сталкивается со льдом, автомобиль подчиняется первому закону Ньютона и съезжает с дороги по прямой, касательной к кривой. Распространенное заблуждение состоит в том, что автомобиль будет двигаться по извилистой дороге за пределами дороги.
[/ hidden-answer]
Во время одной поездки в парке развлечений всадники входят в большую вертикальную бочку и становятся у стены на ее горизонтальном полу. Бочка раскручивается, и пол падает. Всадники чувствуют себя так, как будто они прижаты к стене силой, похожей на силу гравитации. Это сила инерции, которую всадники воспринимают и используют для объяснения событий во вращающейся системе отсчета ствола. Объясните в инерциальной системе отсчета (Земля почти такая), что прижимает всадников к стене, и определите все силы, действующие на них.
Два друга разговаривают. Анна говорит, что спутник на орбите находится в свободном падении, потому что спутник продолжает падать на Землю. Том говорит, что спутник на орбите не находится в свободном падении, потому что ускорение свободного падения не равно
.. С кем вы согласны и почему?
[show-answer q = ”fs-id116503
[скрытый-ответ a = ”fs-id116503
Анна права. Спутник свободно падает на Землю из-за силы тяжести, хотя сила тяжести на высоте спутника слабее, и g — это не
..Свободное падение не зависит от стоимости г ; то есть вы можете испытать свободное падение на Марсе, если спрыгнете с Олимпа (самого высокого вулкана в Солнечной системе).
[/ hidden-answer]
Невращающаяся система отсчета, помещенная в центр Солнца, очень близка к инерциальной. Почему это не совсем инерциальная система отсчета?
Проблемы
(a) Ребенок весом 22,0 кг катается на детской карусели, вращающейся со скоростью 40,0 об / мин. Какая центростремительная сила действует, если он равен 1.25 м от центра? (b) Какая центростремительная сила действует, если карусель вращается со скоростью 3,00 об / мин и находится на расстоянии 8,00 м от ее центра? (c) Сравните каждую силу с его весом.
[show-answer q = ”fs-id116503
[скрытый-ответ a = ”fs-id116503
а. 483 Н; б. 17,4 Н; c. 2,24, 0,0807
[/ hidden-answer]
Вычислите центростремительную силу на конце лопасти ветряной турбины радиусом 100 м, вращающейся на 0.5 об / с. Предположим, что масса 4 кг.
Каков идеальный угол крена для пологого поворота радиусом 1,20 км на шоссе с ограничением скорости 105 км / ч (около 65 миль / ч), если все едут на пределе?
[show-answer q = ”fs-id1165039344901 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165039344901 ″]
[/ hidden-answer]
Какова идеальная скорость для прохождения кривой радиусом 100,0 м с наклоном
?угол?
(а) Каков радиус бобслейного поворота с креном
?и взято на отметке 30.0 м / с при условии идеального наклона? (b) Рассчитайте центростремительное ускорение. (c) Вам кажется это ускорение большим?
[show-answer q = ”fs-id116503
09 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116503
09 ″]
а. 24,6 м; б.
г. 3,73 раза г
[/ hidden-answer]
Часть езды на велосипеде включает в себя наклон под правильным углом при повороте, как показано ниже. Чтобы быть стабильным, сила, действующая на землю, должна быть на линии, проходящей через центр тяжести.Сила, действующая на колесо велосипеда, может быть разделена на две перпендикулярные составляющие: трение параллельно дороге (оно должно обеспечивать центростремительную силу) и вертикальную нормальную силу (которая должна равняться весу системы). (а) Покажите, что
(как показано на рисунке) относится к скорости v и радиусу кривизны r поворота таким же образом, как и для проезжей части с идеальным уклоном, то есть
(б) Вычислить
для 12.0-м / с разворот радиусом 30,0 м (как в гонке).
Если автомобиль движется по крутой кривой на скорости ниже идеальной, необходимо трение, чтобы не допустить скольжения внутрь поворота (проблема на обледенелых горных дорогах). (a) Рассчитайте идеальную скорость, чтобы взять кривую радиусом 100,0 м с наклоном
.. (b) Какой минимальный коэффициент трения необходим для того, чтобы напуганный водитель проехал по той же кривой на скорости 20,0 км / ч?
[show-answer q = ”fs-id1165038980331 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165038980331 ″]
а.16,2 м / с; б. 0,234
[/ hidden-answer]
Современные американские горки имеют вертикальные петли, подобные показанной здесь. Радиус кривизны вверху меньше, чем по бокам, так что центростремительное ускорение вниз вверху будет больше, чем ускорение свободного падения, удерживая пассажиров плотно прижатыми к своим сиденьям. (a) Какова скорость американских горок в верхней части петли, если радиус кривизны там 15,0 м, а ускорение машины вниз равно 1.50 г ? (b) На какой высоте над вершиной петли американские горки должны начинаться из состояния покоя, если трение пренебрежимо мало? (c) Если он действительно начинается на 5,00 м выше, чем ваш ответ на вопрос (b), сколько энергии он потерял на трение? Его масса
.
Ребенок массой 40,0 кг находится в машине с американскими горками, которая движется по петле радиусом 7,00 м. В точке А скорость автомобиля составляет 10,0 м / с, а в точке B — 10,5 м / с. Предположим, что ребенок не держится и не пристегнут ремнем безопасности.(а) Какова сила автомобильного кресла, воздействующая на ребенка в точке А? (b) Какое усилие автомобильного кресла действует на ребенка в точке B? (c) Какая минимальная скорость требуется, чтобы удерживать ребенка на сиденье в точке A?
[показать-ответ q = ”484990 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 484990 ″] a. 179 Н; б. 290 Н; c. 8,3 м / с [/ hidden-answer]
В простой модели Бора основного состояния атома водорода электрон движется по круговой орбите вокруг фиксированного протона.Радиус орбиты
и скорость электрона
Масса электрона
. Какая сила действует на электрон?
Железнодорожные пути следуют круговой кривой радиусом 500,0 м и имеют крен под углом
. Для поездов какой скорости предназначены эти пути?
[показывать-ответ q = ”fs-id116503
[скрытый-ответ a = ”fs-id116503
20.7 м / с
[/ hidden-answer]
Ускоритель частиц в ЦЕРН имеет форму окружности 7,0 км. (а) Какое ускорение протонов
, которые вращаются вокруг ускорителя на
скорости света? (Скорость света
) (б) Какая сила действует на протоны?
Автомобиль объезжает кривую без кренов радиусом 65 м. Если коэффициент статического трения между дорогой и автомобилем равен 0.70, какова максимальная скорость, с которой автомобиль преодолевает поворот без пробуксовки?
[показывать-ответ q = ”fs-id1165039269152 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165039269152 ″]
21 м / с
[/ hidden-answer]
Автодорога с наклоном предназначена для движения со скоростью 90,0 км / ч. Радиус поворота 310 м. Какой угол наклона шоссе?
Глоссарий
- наклонная кривая
- поворот на дороге с уклоном, помогающий автомобилю преодолевать поворот
- центростремительная сила
- любая чистая сила, вызывающая равномерное круговое движение
- Сила Кориолиса
- Сила инерции, вызывающая кажущееся отклонение движущихся объектов при просмотре во вращающейся системе отсчета
- идеальный банк
- наклон кривой дороги, где угол наклона позволяет транспортному средству преодолевать поворот с определенной скоростью без помощи трения между шинами и дорогой; чистая внешняя сила на транспортном средстве равна горизонтальной центростремительной силе в отсутствие трения
- инерционная сила
- Сила, не имеющая физического происхождения
- неинерциальная система отсчета
- ускоренная система отсчета
Третий закон движения Ньютона
Третий закон движения НьютонаДомашнее задание
Глава 5; Третий закон движения Ньютона
Домашнее задание: примеры 6, 8, 11, 12, 13, 14, 17, 19, 23, 24, 25, 28, 32; Pb 1, 2, 3, 6
| Вернуться на домашнюю страницу 3050-х | Назад к календарю | ToC, Ch 5 | Ch 6, Momentum |
Пр. 5.6 Когда вы роняете резиновый мяч на пол, он почти отскакивает. на исходную высоту. Что заставляет мяч отскакивать?
Пол воздействует на мяч направленной вверх силой — это останавливает мяч и дает ему ускорение вверх.
Эта направленная вверх сила от пола вызывает деформацию или изменение мяча. форма, пока она соприкасается с полом.
Ex 5.8 Два груза 100-N прикреплены к пружинной шкале, как показано.Показывает ли шкала ноль, 100 Н или 200 Н — или какое-то другое значение?
Шкала показывает натяжение струны. Напряжение в длина струны 100 Н. Это сила, которую струна должна приложить. вверх на любой из гирь 100-N на любом конце струны.
Ничего не движется, ничего не ускоряется, поэтому чистая сила на весне ноль. Аналогично, чистая сила на любом весов 100-N также равен нулю.Но это другой вопрос. Весна Весы не измеряют чистую силу . Весенняя шкала просто измеряет напряжение , величину сила, оказываемая струной.
Пример 5.11 Почему на педали велосипеда можно прикладывать большее усилие? если потянуть за руль?
Руль затем тянет вниз на вас, как будто кто-то толкали вниз на ваших плечах.Это позволяет вам большее вниз усилие на педалях
Пример 5.12 Бейсбольная бита замедляется при ударе по мячу?
Конечно. Когда бита оказывает давление на бейсбольный мяч, бейсбольный мяч также оказывает на биту силу — в обратном направлении.
Пример 5.13 Почему альпинист тянет веревку вниз, чтобы двигаться вверх?
Когда альпинист тянет вниз на веревке, веревка тянет вверх на альпиниста.Это еще один хороший пример Третьего закона Ньютона или Закон действия и противодействия.
Пр. 5.14 Вы толкаете тяжелую машину вручную. Автомобиль, в свою очередь, отталкивает с противоположной, но равной силой на вас. Разве это не значит, что силы отменяются? друг друга, делая ускорение невозможным?
Чтобы «нейтрализовать друг друга», две силы должны были бы воздействовать на тот же объект. Силы действия-противодействия, о которых мы говорим с помощью Третьего закона Ньютона — или силы в этом вопросе — действовать на различных объектов.
Пример 5.17. Предположим, летят две тележки, одна в два раза массивнее другой. при отпускании соединяющей их сжатой пружины. Как быстро более тяжелая тележка по сравнению с более легкой тележкой?
Согласно Третьему закону Ньютона силы, действующие на эти две массы, должны быть равны. (и в противоположных направлениях). Согласно шкале Ньютона Second Закон, F = m a, находим a = F / m. Это означает ускорение вдвое более массивного тележка будет одна половина разгон другой.
Пример 5.19 Если грузовик Mack и Honda Civic столкнулись лицом к лицу, на какое транспортное средство сила удара больше? Какой автомобиль испытывает большее ускорение?
force будет таким же на двух машинах, согласно Третьему закону Ньютона. Это означает, что Civic с намного меньшая масса, будет испытать намного большее ускорение , согласно второму закону Ньютона.
Пр. 5.23 Представьте себе перетягивание каната на гладком полу между мальчиками, носящими носки и девушки в обуви на резиновой подошве. Почему девушки побеждают?
Девушки могут проявлять большую силу с помощью обуви на резиновой подошве, поэтому они Выиграет.
Пр. 5.24 Два человека равной массы пытаются перетянуть канат с 12-метровым каналом. веревка стоя на льду без трения. Когда они тянут веревку, каждый из них скользят навстречу друг другу. Как соотносятся их ускорения и как далеко каждый человек скользит перед встречей?
Сила на каждом будет одинакова, поэтому у них всегда будет одинаковое ускорение. — и, следовательно, с одинаковой скоростью, и они будут перемещаться на одинаковое расстояние.Таким образом, они встретятся посередине, поэтому каждому придется пройти 6 метров.
Пример 5.28 Когда сумма двух векторов равна нулю, как они должны быть связаны?
Они должны быть равны по величине и ровно напротив в направление.
Пример 5.32 Если вы стоите в автобусе, который движется с постоянной скоростью и уроните мяч из протянутой руки, вы увидите его путь как вертикальный прямая линия. Каким будет путь другу, стоящему сбоку дорога?
Друг у дороги увидит горизонтальную составляющую его движения.Он / она может описать это, сказав, что он движется по «дуге» или по «криволинейный путь». Внимательное наблюдение покажет, что он движется по «параболический путь». Мы поговорим об этом подробнее в следующей главе. по нелинейному движению.
Pb 5.1 Боксер пробивает в воздухе лист бумаги и вылетает из него. отдых до скорости 25 м / с за 0,05 с. Если масса бумаги 0,003 кг (то есть 3 грамма), какое усилие на него прикладывает боксер?
F = m a
Но какое ускорение, а?
а = v / т
a = (25 м / с) / (0.05 с)
a = 500 м / с / с
a = 500 м / с
Pb 5.2 Если вы стоите у стены на скейтборде без трения и толкайте стену с силой 30 Н, насколько сильно стена давит на вас? Если твой масса 60 кг, какое у вас ускорение?
Из Третьего закона Ньютона мы знаем, что стена реагирует на , давя на нее. вы с силой 30 Н.
F = 30 N
Из Второго закона Ньютона мы можем вычислить ускорение, которое производит,
F = ma
а = Ф / м
a = (30 Н) / (60 кг)
а = 0.5 м / с 2
Pb 5.3 Если капли дождя падают вертикально со скоростью 3 м / с и вы бегая со скоростью 4 м / с, как быстро они попадают в ваше лицо?
Для этого нам понадобится векторная диаграмма сложения. Пока капли дождя падают вниз со скоростью 3 м / с, они также движутся горизонтально со скоростью 4 м / с, потому что вы бежите по горизонтали со скоростью 4 м / с. Нарисуем векторы (или стрелки) для обозначения этих скоростей,
Вы можете начать с рисования вектора скорости сначала вниз на 3 м / с, а затем, в конце этого вектора, начните скорость 4 м / с горизонтальный вектор.Результирующий вектор — это вектор, который вы рисуете, который начинается где ваша диаграмма начинается и заканчивается там, где ваша диаграмма заканчивается.
Или вы можете подумать о том, чтобы начать с рисования горизонтальной оси 4 м / с. сначала вектор, а затем, в конце этого вектора, начните движение вниз на 3 м / с вектор скорости. Результирующий вектор — это вектор, который вы рисуете, который начинается где ваша диаграмма начинается и заканчивается там, где ваша диаграмма заканчивается.
Для всех этих векторных диаграмм сложения результат , векторная сумма этих двух скоростей составляет 5 м / с под углом 37 градусов. от горизонтали.
Pb 5.6 Каноэ плывет со скоростью 4 км / ч прямо через реку, которая протекает на скорости 3 км / ч, как показано на рисунке.
а) Какова результирующая скорость каноэ относительно берега?
Это требует другой диаграммы сложения векторов. Это очень много как и предыдущий!
Для любой из этих векторных диаграмм чистый результат, , результат , векторная сумма этих скоростей такова, что каноэ движется через реку со скоростью 5 км / ч под углом 37 градусов к югу от востока или 53 градуса к востоку от юга (или 37 градусов, как показано на схеме).
(b) Примерно в каком направлении следует грести каноэ добраться до пункта назначения через реку?
| Вернуться на домашнюю страницу 3050-х | Назад к календарю | ToC, Ch 5 | Ch 6, Momentum |Конечно, для этого потребуется еще одна диаграмма сложения векторов. Но этот веселее. Мы хотим, чтобы результат был горизонтальным (или восточным). Мы знаем, как быстро может ехать на каноэ (это 4 км / ч), но мы не знаем направление . На какое направление нужно ли грести каноэ со скоростью 4 км / ч, чтобы, когда река течет вниз (или на юг) на скорости 3 км / ч, результирующая скорость будет горизонтальной. (или восток)?
Типичные вопросы с несколькими ответами:
1.Силы действия-противодействия, с которыми мы сталкиваемся в Третьем законе Ньютона
.а) всегда компенсируют друг друга.
б) всегда действуют на разные объекты.
c) всегда такие же, как силы трения и опоры.
г) могут быть перпендикулярны друг другу.
2. Применяется третий закон Ньютона.
а) только неподвижным объектам (например, толканию по стене)
b) к парам предметов, из которых хотя бы одна должна быть в состоянии покоя (например, нанесение удара по стена с движущимся мячом)
c) к любым двум объектам, которые взаимодействуют
d) только для пар объектов, у которых один намного массивнее другого.
3. Третий закон Ньютона —
.а) частный случай второго закона Ньютона.
б) частный случай Первого закона Ньютона.
c) независимо от других законов движения Ньютона.
d) применяется только в том случае, если сопротивлением воздуха можно пренебречь.
4. Результат двух векторов равен
.а) меньший из двух векторов.
б) среднее значение двух векторов.
c) векторная сумма двух векторов.
d) больший из двух векторов.
5. Можно добавлять векторы
| Вернуться на домашнюю страницу 3050-х | Назад к календарю | ToC, Ch 5 | Ch 6, Momentum |а) как обычные числа.
б) путем умножения их величин.
c) путем вычитания их величин и умножения их единиц.
г) путем построения диаграммы сложения векторов.
Типичные вопросы с ответами на несколько вариантов ответа:
1.Силы действия-противодействия, с которыми мы сталкиваемся в Третьем законе Ньютона
.а) всегда компенсируют друг друга.
б) всегда воздействовать на разные объекты.
c) всегда такие же, как силы трения и опоры.
г) могут быть перпендикулярны друг другу.
2. Применяется третий закон Ньютона.
а) только неподвижным объектам (например, толканию по стене)
b) к парам предметов, из которых хотя бы одна должна быть в состоянии покоя (например, нанесение удара по стена с движущимся мячом)
c) к любым двум объектам, которые взаимодействуют
d) только для пар объектов, у которых один намного массивнее другого.
3. Третий закон Ньютона —
.а) частный случай второго закона Ньютона.
б) частный случай Первого закона Ньютона.
c) независимо от других законов движения Ньютона.
d) применяется только в том случае, если сопротивлением воздуха можно пренебречь.
4. Результат двух векторов равен
.а) меньший из двух векторов.
б) среднее значение двух векторов.
c) векторная сумма двух векторов.
d) больший из двух векторов.
5. Можно добавлять векторы
| Вернуться на домашнюю страницу 3050-х | Назад к календарю | ToC, Ch 5 | Ch 6, Momentum |а) как обычные числа.
б) путем умножения их величин.
c) путем вычитания их величин и умножения их единиц.
г) путем построения диаграммы сложения векторов.
(C) 2003, Дуг Дэвис; все права защищены
Понимание взаимосвязи между силой и ускорением
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.

 Весы содержат пружины, которые сжимаются пропорционально вашему весу — подобно резиновым лентам, расширяющимся при натяжении.
Весы содержат пружины, которые сжимаются пропорционально вашему весу — подобно резиновым лентам, расширяющимся при натяжении.
