почему нештрафуемый порог +20 км/ч нельзя отменять :: Autonews
Моя позиция как автора действующей нормы о ненаказуемых 20 км/ч, которую поддержала фракция «Единая Россия», такова: сначала правительство должно провести тотальный аудит улично-дорожной сети, включая проверку разметки и дорожных знаков на предмет их соответствия дорожной обстановке, федеральным законам и ПДД, обоснованность ограничений скоростного режима и расстановку камер.
К сожалению, в России стало нормой устанавливать ничем не обоснованные ограничения скоростного режима в паре с камерами не там, где это необходимо для обеспечения безопасности и профилактики нарушений, а там, где легче собрать штрафные деньги. Это самые настоящие ловушки для водителей. Нередко из ниоткуда появляются знаки с ограничением скорости 40 км в час. А до этого, представьте, водители ехали с разрешенной скоростью 90–110 км в час.
Далее необходимо поднять скоростной режим там, где он не соответствует категории дороги. Сейчас в России он значительно занижен. На Кутузовском проспекте в Москве скорость ограничена 80 км/ч, но сейчас благодаря поправке +20 км/ч по нему можно ехать более-менее прилично. А власти еще хотят снизить порог до 60 км в час.
А почему я должен ехать по добротному Минскому шоссе до Белоруссии 90 км/ч, а уже за границей по такой же дороге могу законно передвигаться со скоростью 120 км/ч плюс 10 км в час? Если у нас снизить до +10 км/ч, мы по такой же дороге сможем ехать только со скоростью 100 км в час. Почему мы должны ездить медленнее на 30 км/ч, чем водители в соседней стране на трассах того же качества? Что за издевательство? Я считаю, что на трассе М-9 водителей специально провоцируют, чтобы они нарушали. Там хорошая дорога, гаишников мало, камер тоже негусто.
А еще на некоторых участках стоит система «Автодория» родом из Татарстана, которая незаконно измеряет среднюю скорость — камеры стоят при въезде и при выезде с участка в 30–50 километров. И люди получают штрафы, хотя в законодательстве нет понятия «средняя скорость». Есть нарушение скоростного режима с конкретными цифрами: 20–40 км/ч, 40–60, 60–80 и свыше 80 км в час. Кроме всего прочего, у нас есть и перевозчики, которые несут убытки из-за того, что суточный пробег в России у них в два раза меньше, чем по Европе.
Фото: ГК «Автодор»
Есть и еще одно необходимое изменение. Необходимо вернуть Госавтоинспекции полномочия по согласованию планов и проектов организации дорожного движения. Сейчас организацией дорожного движения занимаются органы исполнительной власти регионов — это местные департаменты и министерства транспорта. И получается, что чиновники на местах сами расставляют знаки, наносят разметку, ставят камеры, сами собирают деньги и при этом сами себя же контролируют. Это недопустимо!
Сейчас организацией дорожного движения занимаются органы исполнительной власти регионов — это местные департаменты и министерства транспорта. И получается, что чиновники на местах сами расставляют знаки, наносят разметку, ставят камеры, сами собирают деньги и при этом сами себя же контролируют. Это недопустимо!
Раньше ГИБДД могла проводить независимую оценку планов организации дорожного движения. Сейчас же государственная контрольно-надзорная вертикаль в лице МВД разрушается, министерство готово охотно передать свои полномочия регионам (читай: людям с улицы), и это крайне опасно. Ведь нередко организация дорожного движения во многих субъектах противоречит существующим нормам. Это происходит потому, что власти в этих субъектах заинтересованы в максимальном сборе штрафных денег. То есть главной целью ставится не организация дорожного движения и дорожная безопасность, а сбор денег с автомобилистов всеми возможными путями.
Например, в Москве множество мест, где стоянка или остановка автомобиля не создает помех другим участникам дорожного движения, но стоянка или остановка там запрещены. И наоборот, там, где стоянка или остановка прямо запрещены ПДД, устроена платная парковка. Этот подход, который я называю тотальной коммерциализацией, недопустим. Он создает социальное напряжение в обществе, озлобляет людей, формирует правовой нигилизм. Это нагрев социального котла.
И наоборот, там, где стоянка или остановка прямо запрещены ПДД, устроена платная парковка. Этот подход, который я называю тотальной коммерциализацией, недопустим. Он создает социальное напряжение в обществе, озлобляет людей, формирует правовой нигилизм. Это нагрев социального котла.
Поэтому сначала надо решить все вышеописанные проблемы и только потом ставить вопрос о возможном снижении нештрафуемого порога скорости. Во фракции «Единая Россия» придерживаются именно такой точки зрения, такой последовательности приоритетов. Если всего перечисленного сделано не будет, Госдума, уверен, снижение нештрафуемого порога не поддержит.
Сейчас правительство РФ готовит новую редакцию КоАПа с обновленным текстом, измененными санкциями и нормами — это дело небыстрое. Черновой вариант будет готов в лучшем случае в конце следующего года. После чего его будут дорабатывать. На принятие Госдумой тоже понадобится время. В целом, по моему прогнозу, новый КоАП появится не ранее чем через пару лет. У всех нас есть время, чтобы подготовиться.
У всех нас есть время, чтобы подготовиться.
Страница 8 (учебник Моро 2 часть 4 класс) ответы по математике
27. Составь по таблице три задачи и реши их.1) Автомобиль двигался со скоростью 60 км/ч в течение 2 часов. Какое расстояние от проехал за это время?
60 * 2 = 120 км.Ответ: 120 км.
2) Автомобиль проехал 120 км со скоростью 60 км/ч. Сколько времени он затратил на этот путь?
120 : 60 = 2 ч.Ответ:: 2 ч.
3) Автомобиль проехал 120 км за 2 ч. С какой скоростью он двигался?
120 : 2 = 60 км/ч.Ответ: 60 км/ч.
скорость, зная расстояние и время;
расстояние, зная скорость и время;
время, зная скорость и расстояние.
скорость = расстояние : время;
расстояние = скорость * время;
время = расстояние : скорость.
1) За 1 ч (60 мин), двигаясь с одинаковой скоростью, машина проходит 60 км. Сколько километров она пройдёт за 10 мин?
2) Поезд, двигаясь с одинаковой скоростью, прошёл 1 км за 1 мин. За сколько времени он пройдёт 15 км ? 60 км?
3) Составь задачу по чертежу и реши её.
1)
1) 60 : 60 = 1 (км/мин) − скорость машины
2) 1 * 10 = 10 (км) пройдет машина за 10 минут
Ответ: 10 км.2)
1) 15 : 1 = 15 (мин) − будет идти поезд 15 км
2) 60 : 1 = 60 (мин) = 1 (ч) − будет идти поезд 60 кмОтвет: 15 км за 15 мин, 60 км за 1 ч.
3)
Два велосипедиста выехали на встречу друг другу, и встретились через 3 ч. Какое расстояние они проехали, если скорость первого велосипедиста 18 км/ч, a второго 15 км/ч.
1) 18 * 3 = 54 (км) − проехал до встречи первый велосипедист
2) 15 * 3 = 45 (км) − проехал до встречи второй велосипедист
3) 54 + 45 = 99 (км) они проехалиОтвет: 99 км.
1) За 4 одинаковых велосипеда заплатили к р. Сколько стоят 9 таких велосипедов?
2) Составь задачу по выражению (с : 5) * 3.
1) k : 4 * 9.
2) За 5 карандашей заплатили 100 р. Сколько стоят три таких карандаша?
100 : 5 * 3 = 60 p.Ответ: 60 p.
1) 13 — 7 = 6 ч машина была в пути.
2) 240 : 6 = 40 км/ч скорость машины.Ответ: 40 км/ч.
1) 1667 + 1 524 = 3191 км расстояние от Москвы до Новосибирска.
2) 5042 — 3191 = 1851 км расстояние от Новосибирска до Иркутска.Ответ: 1851 км.
3 * (14 + 8) : 2 = 3 * 22 : 2 = 66 : 2 =
7 * (12 + 9) : 3 = 7 * 21 : 3 = 147 : 3 = 49
82000 − 4730 * 8 = 82000 − 37840 = 44160
93000 − 8691 * 7 = 93000 − 60837 = 32163
Доехать по трассе «Таврида» от Керчи до Севастополя можно будет уже в сентябре — Российская газета
Открыть рабочее движение по всей длине четырехполосной трассы «Таврида» от Керчи до Севастополя можно будет уже через месяц. Об это сообщил Григорий Назаров, пресс-секретарь АО «Высококачественные автомобильные дороги» («ВАД») — генерального подрядчика строительства трассы «Таврида». Это будет практически революционное событие для полуострова. Новая автодорога уже обеспечила основной поток туристов на полуостров, а скоро она же даст возможность местным жителям и гостям свободно путешествовать по всему полуострову.
«Рабочее движение — это полноценное движение на дороге, где продолжаются те или иные работы — обустраивают пешеходные переходы, разбирают леса на эстакадах и так далее, — пояснил Григорий Назаров. — Из-за этого бывают частичные перекрытия, локальные участки с ограничением скорости до 40 км/ч. Однако по сути дорога — работает. Строители могли бы дождаться полного завершения работ и только потом разрешить движение. Но их бы все прокляли — людям нужна дорога, она есть, по ней можно безопасно ездить — зачем же ее держать под шлагбаумом?!»
— Из-за этого бывают частичные перекрытия, локальные участки с ограничением скорости до 40 км/ч. Однако по сути дорога — работает. Строители могли бы дождаться полного завершения работ и только потом разрешить движение. Но их бы все прокляли — людям нужна дорога, она есть, по ней можно безопасно ездить — зачем же ее держать под шлагбаумом?!»
Пока что трасса в рабочем режиме открыта от Керчи до Симферополя. Это 129 километров хорошей четырехполосной дороги с разделительным отбойником, отсутствием пересечений на одном уровне и разрешенной скоростью до 90 км/ч. Проектом предусмотрено 120 км/ч и дорожники намекают, что у ГИБДД есть некоторые планы в этом отношении, но они по не раскрывают их.
Участок от Симферополя до Севастополя протяженностью в шесть десятков километров, включая объездную столицы Крыма, собираются запустить в сентябре. Тоже, пока в рабочем режиме, но по трассе можно будет проехать от одного конца до другого.
«Исторически сложилось, что в Крыму вся транспортная инфраструктура строилась в меридиональном направлении — от Перекопа до Симферополя и дальше по всем городам, — объяснил начальник службы автодорог Крыма Александр Нефедов. — Сейчас же поток приходит с востока, через Керчь. Но инфраструктура на это рассчитана не была, поэтому нам важно было запустить «Тавриду» вместо тех узких дорог, которые были раньше между столицей Крыма и Керчью. Теперь настал черед Севастополя».
— Сейчас же поток приходит с востока, через Керчь. Но инфраструктура на это рассчитана не была, поэтому нам важно было запустить «Тавриду» вместо тех узких дорог, которые были раньше между столицей Крыма и Керчью. Теперь настал черед Севастополя».
Сейчас работы на всей трассе «Таврида» завершены на 95%, сообщили в «ВАД». На участке от Крымского моста до Симферополя открыто рабочее движение, работы продолжаются в основном на надземных пешеходных переходах, площадках отдыха, некоторых развязках с местными дорогами, устанавливаются шумозащитные ограждения. Полностью закончен, но пока не открыт, северный обход Симферополя. Его запустят вместе с Севастопольским участком дороги — без него он будет, по сути, тупиковым. Там осталось проложить около 20 километров асфальта. Дорожники уже прошли путь от Севастополя до места с романтическим названием Приятное свидание. И до Симферополя осталось уже совсем не много.
«Раньше от Керчи до Приморского — это чуть раньше Феодосии — шла двухрядная дорога, вместо которой сейчас создана новая четырехполоска, — объяснил Григорий Назаров. — Потом шоссе сворачивало к Феодосии, шло вдоль моря, через курортные зоны и поселки до Белогорска. Этот кусок: Приморское — Белогорск — мы построили заново по целине. И далее до Симферополя шла узкая двухрядная дорога, теперь она перестроена в современную четырехрядку».
— Потом шоссе сворачивало к Феодосии, шло вдоль моря, через курортные зоны и поселки до Белогорска. Этот кусок: Приморское — Белогорск — мы построили заново по целине. И далее до Симферополя шла узкая двухрядная дорога, теперь она перестроена в современную четырехрядку».
Как говорят старожилы, если раньше путь от Керчи до Симферополя мог занимать пять часов при хорошем раскладе и девять при плохом, то теперь стабильно чуть больше двух.
При этом трасса «Таврида» уже обеспечила прибытие в Крым большей части выбравших местом отдыха республику туристов. Еще в июле, когда после ослабления коронавирусных ограничений, на нее хлынул поток отдыхающих из всех регионов России. В министерстве курортов и туризма республики подсчитали, что за месяц в Крым приехали 352,6 тысячи легковых машин, обеспечив прибытие 64% всех отдыхающих. Еще 31% добрался самолетом, а 5% — поездом, добавили в ведомстве. Так что «Таврида» еще до окончания строительства стала главными воротами полуострова.
Окончательно трассу «Таврида» откроют для автомобилистов только в конце года
При укладке трассы «Таврида» дорожники используют уникальный щебеночно-мастичный асфальт. В «ВАД» уверяют, что его состав специально был подобран для этой дороги, крымского климата и предстоящих условий эксплуатации. В любом случае, за дорогой пристально следят, и пробы — керны — с каждого уложенного участка трассы отправляются в лабораторию. Там проверяют и состав, и плотность укладки, и другие параметры. На пробы с «Тавриды», уверяют в «ВАД», нареканий ни разу не было.
В «ВАД» уверяют, что его состав специально был подобран для этой дороги, крымского климата и предстоящих условий эксплуатации. В любом случае, за дорогой пристально следят, и пробы — керны — с каждого уложенного участка трассы отправляются в лабораторию. Там проверяют и состав, и плотность укладки, и другие параметры. На пробы с «Тавриды», уверяют в «ВАД», нареканий ни разу не было.
Для человека, который приехал в Крым отдыхать за рулем своей машины, пока что дорога воспринимается так: после съезда с легендарного Крымского моста ты вдруг оказываешься на быстрой и удобной трассе с ограничением скорости в 90 км/ч. После кубанских однополосных дорог, очереди на переезд в Тимашевске или объезда его по задворкам города, пробок перед пунктами оплаты на М4 — сплошное удовольствие. И продолжается это счастье ровно 195 км, пока ты не упираешься в пригороды Симферополя. В принципе если абстрагироваться от пейзажа, очень похоже на въезд в столицу в воскресенье вечером по какому-нибудь Осташковскому шоссе — жарко, все стоят, движения нет, жизни нет, зато вокруг тебя машины из всех регионов России. Часок потерпеть — и откроется Южнобережное шоссе, довольно шустрое и красивое. Юго-восточный обход Симферополя тоже планируется, но он появится не раньше 2023 года, сказал начальник крымских автодорог Александр Нефедов.
Часок потерпеть — и откроется Южнобережное шоссе, довольно шустрое и красивое. Юго-восточный обход Симферополя тоже планируется, но он появится не раньше 2023 года, сказал начальник крымских автодорог Александр Нефедов.
«Запуск северного обхода Симферополя и участка до Севастополя очень сильно разгрузит столицу Крыма и упростит проезд во все направления, — продолжил Нефедов. — Сейчас через город едут все — и кому надо в Ялту, и в Севастополь, и в Евпаторию, и к аэропорту, в Джанкой… А у нас на Северном обходе есть Евпаторийская развязка, откуда можно уехать и в северном направлении, и в западном, и к аэропорту. За счет этого нагрузка на улицы снизится и проехать в любую сторону станет проще».
Инфографика «РГ» / Антон Переплетчиков / Алексей Дуэль
Между тем
Российские туристы приобрели за месяц более 10 тысяч единых билетов в города-курорты Крымского полуострова и обратно, сообщили в минтрансе. Чаще всего они ездили в Феодосию и Судак.
Мультимодальные перевозки туристов в Крым из регионов, не имеющих прямого железнодорожного сообщения с полуостровом, возобновились 10 июля. Единый билет включает проезд сразу несколькими видами транспорта — железнодорожным, воздушным и автомобильным. Путешественникам это дает ряд преимуществ. Единый билет гарантирует перевозку на всем пути следования, обеспечивает максимально удобную стыковку между рейсами. В результате сокращается время ожидания и количество пересадок. Купить такой проездной документ можно в железнодорожных и авиационных кассах, в терминалах и через агентскую сеть По всей стране действует более семи тысяч пунктов оплаты. Билет также можно оформить онлайн.
Единый билет включает проезд сразу несколькими видами транспорта — железнодорожным, воздушным и автомобильным. Путешественникам это дает ряд преимуществ. Единый билет гарантирует перевозку на всем пути следования, обеспечивает максимально удобную стыковку между рейсами. В результате сокращается время ожидания и количество пересадок. Купить такой проездной документ можно в железнодорожных и авиационных кассах, в терминалах и через агентскую сеть По всей стране действует более семи тысяч пунктов оплаты. Билет также можно оформить онлайн.
Подготовил Евгений Гайва
Кстати
При прокладке трассе «Таврида» строители случайно наткнулись на уникальную карстовую полость. Экскаваторщик, готовя площадку для насыпи, пробил ковшом свод зала высотой 14 метров. Дорожники позвали ученых из Крымского госуниверситета. Те провели исследования и обнаружили невероятные находки: уникальные минералогические образования, удивительные микрорганизмы, пещерное захоронение ископаемых животных и многое другое. Пещеру назвали «Таврида», над ней построили своеобразный мост, держащий огромную защитную плиту — по ней и прошла трасса. А саму пещеру стали готовить для посещения туристами. Предполагается, что это будет едва ли не единственная в мире подземная полость, доступная даже для инвалидов-колясочников.
Пещеру назвали «Таврида», над ней построили своеобразный мост, держащий огромную защитную плиту — по ней и прошла трасса. А саму пещеру стали готовить для посещения туристами. Предполагается, что это будет едва ли не единственная в мире подземная полость, доступная даже для инвалидов-колясочников.
Водители, проезжая по трассе «Таврида» рядом с поселком Зуя, вряд ли могут хотя бы заподозрить, что под колесами их машин 14 метров пустоты. Но они там есть.
Расстояние от Орджоникидзе до Симеиза
Ниже представлен маршрут движения, указано расстояние. Также можно прикинуть сколько времени займет поездка и рассчитать ее стоимость в зависимости от расхода топлива транспортного средства или цены за километр.
Сколько км от Орджоникидзе до Симеиза
По дорогам, в км.
220
По прямой, в км.
120
Симеиз находится в 220 километрах от Орджоникидзе если ехать по дорогам и трассам общего пользования. Маршрут движения отмечен линией синего цвета на карте выше.
По прямой расстояние 120 километров.
Таблица расстояний между городами Крыма.
Маршрут движения отмечен линией синего цвета на карте выше.
По прямой расстояние 120 километров.
Таблица расстояний между городами Крыма.Сколько времени ехать от Орджоникидзе до Симеиза
Зависит от вида транспорта. Быстрее всего добраться на автомобиле, дорога до Симеиза займет 2 часа 45 минут (без учета пробок, при средней скорости 80 км/ч).
На своем авто:Расход топлива, в литрах
{{Math.ceil(own_auto_fuel)}}
Стоимость поездки (примерно), в ₽
{{Math.ceil(own_auto_cost/10)*10}}
Расчет примерной стоимости поездки при указанной цене топлива:
- При расходе {{own_auto_consumption}} литров на 100 километров стоимость поездки — {{Math.

Стоимость поездки (примерно), в ₽
{{taxi_auto_cost}}
Расчет примерной стоимости поездки при указанной цене за 1 километр:
- При цене {{price}} ₽ за 1 километр стоимость поездки — {{price*distance+taxi_auto_price_landing}} ₽
Если ехать на автобусе (при средней скорости 65 км/ч), то вы будете в Симеизе через 3 часа 23 минуты.
На велосипеде, двигаясь со средней скоростью 20 км/ч, это расстояние проедите за 11 часов.
Отправляясь пешком по дорогам, Вы потратите на этот путь 1 день 20 часов (без учета времени потраченного на остановки).
Расстояния от Орджоникидзе до других городов и поселков Крыма
Расстояние от Орджоникидзе до Бахчисарая
Ниже представлен маршрут движения, указано расстояние. Также можно прикинуть сколько времени займет поездка и рассчитать ее стоимость в зависимости от расхода топлива транспортного средства или цены за километр.
Сколько км от Орджоникидзе до Бахчисарая
По дорогам, в км.
150
По прямой, в км.
120
Бахчисарай находится в 150 километрах от Орджоникидзе если ехать по дорогам и трассам общего пользования. Маршрут движения отмечен линией синего цвета на карте выше. По прямой расстояние 120 километров. Таблица расстояний между городами Крыма.Сколько времени ехать от Орджоникидзе до Бахчисарая
Зависит от вида транспорта. Быстрее всего добраться на автомобиле, дорога до Бахчисарая займет 1 час 52 минуты (без учета пробок, при средней скорости 80 км/ч).
Быстрее всего добраться на автомобиле, дорога до Бахчисарая займет 1 час 52 минуты (без учета пробок, при средней скорости 80 км/ч).
Расход топлива, в литрах
{{Math.ceil(own_auto_fuel)}}
Стоимость поездки (примерно), в ₽
{{Math.ceil(own_auto_cost/10)*10}}
Расчет примерной стоимости поездки при указанной цене топлива:
- При расходе {{own_auto_consumption}} литров на 100 километров стоимость поездки — {{Math.ceil(own_auto_consumption*distance/100*own_auto_price_per_liter/10)*10}} ₽
Стоимость поездки (примерно), в ₽
{{taxi_auto_cost}}
Расчет примерной стоимости поездки при указанной цене за 1 километр:
- При цене {{price}} ₽ за 1 километр стоимость поездки — {{price*distance+taxi_auto_price_landing}} ₽
Если ехать на автобусе (при средней скорости 65 км/ч), то вы будете в Бахчисарае через 2 часа 18 минут.
На велосипеде, двигаясь со средней скоростью 20 км/ч, это расстояние проедите за 7 часов 30 минут.
Отправляясь пешком по дорогам, Вы потратите на этот путь 1 день 6 часов (без учета времени потраченного на остановки).
Расстояния от Орджоникидзе до других городов и поселков Крыма
Задачи на движение
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Предварительные навыкиЗадача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
Ответ: за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
Ответ: вертолет был в пути 5 часов.
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80 : 40 = 2
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60 : 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ: скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700 : 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400 : 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40 : 20 = 2
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15 : 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204 : 12 = 17 ч
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102 : 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110 : 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
56 : 8 = 7 ч
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20 : 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
80 : 10 = 8 ч
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72 : 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72 : 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72 : 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
110 : 22 = 5 ч
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Решение
Найдем скорость удаления велосипедистов
11 + 13 = 24 км
Узнаем какое расстояние будет между ними через 4 часа
24 × 4 = 96 км
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
510 : 102 = 5 ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?Решение
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
60 : 15 = 4 ч
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
120 : 30 = 4 ч
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Какое расстояние было между велосипедистами первоначально?
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
Ответ: между велосипедистами первоначально было 18 км.
Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
48 : 12 = 4 ч
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Задачи на движение. Задачи на сближение и удаление Скорость сближения
Содержание урокаЗадача на нахождение расстояния/скорости/времени
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
Ответ : за 3 часа автомобиль проедет 240 километров.
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180: 3 = 60 км/ч
Ответ : скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96: 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72: 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ : автомобиль двигался быстрее велосипедиста в 4 раза.
Задача 4 . Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600: 120 = 5 часов
Ответ : вертолет был в пути 5 часов.
Задача 5 . Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
Ответ : за 6 часов вертолет преодолел 960 км.
Задача 6 . Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228: 4 = 57 км/ч
Ответ : скорость автомобиля в оставшееся время составляла 57 км/ч
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м , а второго — 105 м/м , то скорость сближения будет составлять 100 + 105 , то есть 205 м/м . Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ : расстояние между населенными пунктами составляет 44 км.
Задача 2 . Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60: 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ : велосипедисты встретились через 2 часа.
Задача 3 . Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32: 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ : через 2 часа расстояние будет между поездами будет 440 километров.
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
Ответ : через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
Задача 3 . Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80: 40 = 2
Ответ : через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4 . Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60: 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ : скорость мотоциклиста составляла 30 км/ч.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления .
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1 . Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ : через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700: 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.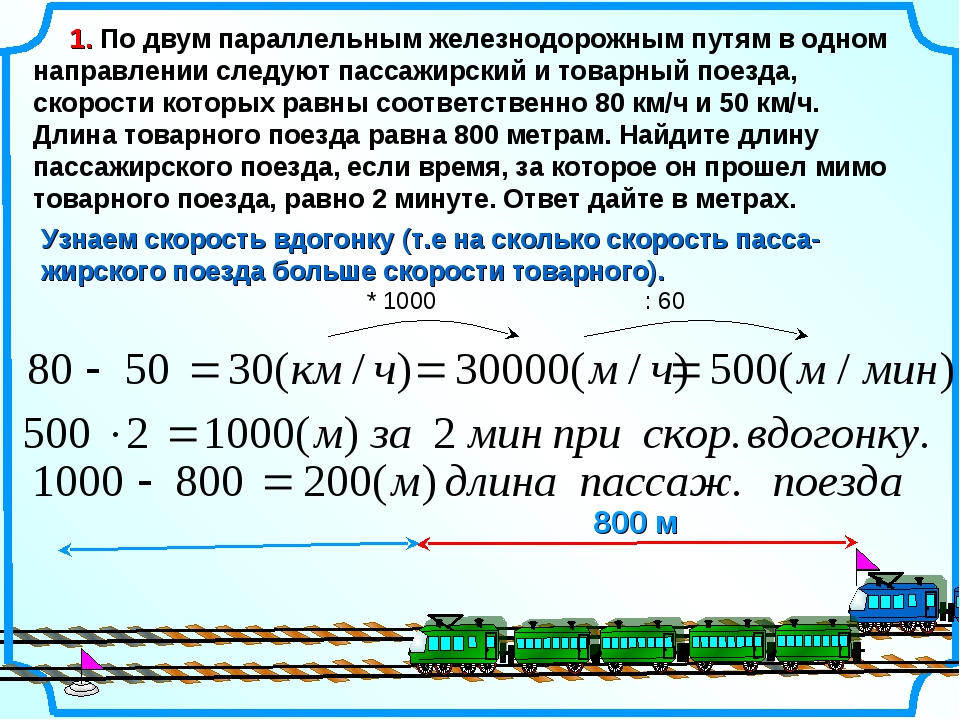
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400: 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2 . Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40: 20 = 2
Ответ : автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью .
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
по течению реки , и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.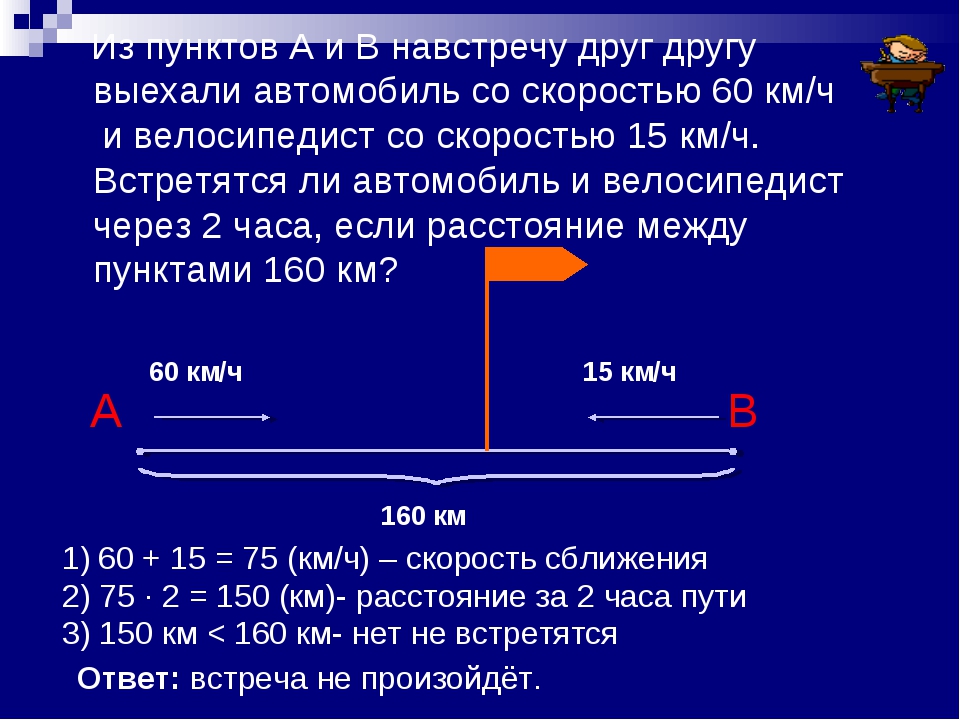
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки , и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1 . Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2 . Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3 . Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4 . За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15: 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204: 12 = 17 ч
Ответ : теплоход пройдет 204 километра за 17 часов
Задача 5 . Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102: 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6 . Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110: 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ : собственная скорость лодки составляет 26 км/ч
Задача 7 . За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
Для этого расстояние (56км) разделим на скорость движения лодки:
56: 8 = 7 ч
Ответ : при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20: 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В . Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
Для этого расстояние (80км) разделим на скорость движения (10км/ч)
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72: 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки.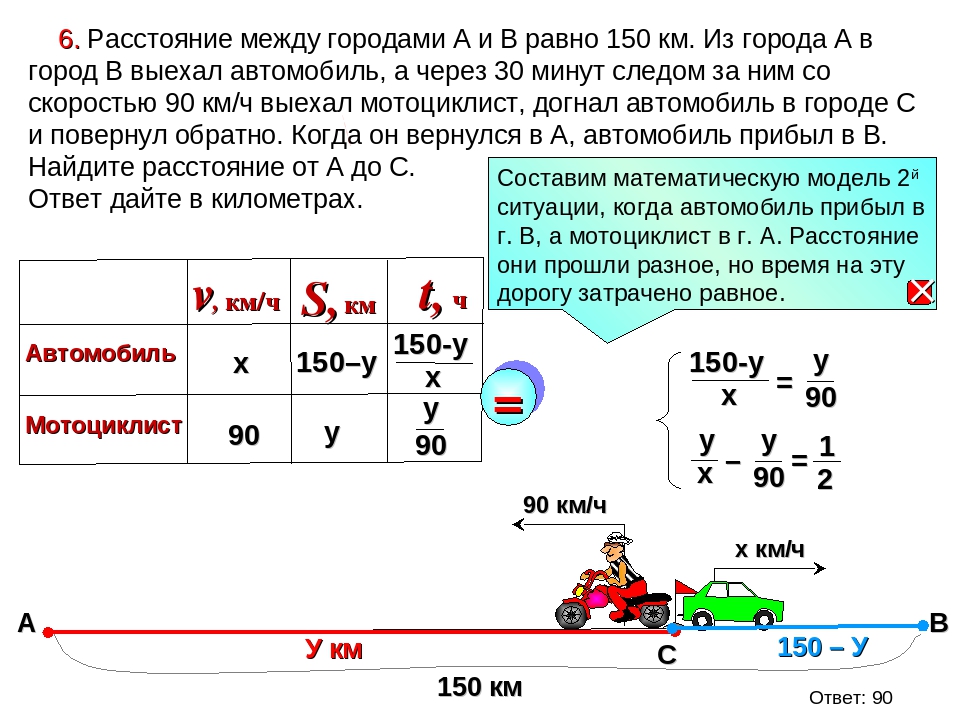 В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72: 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72: 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
Задача 5.
Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста.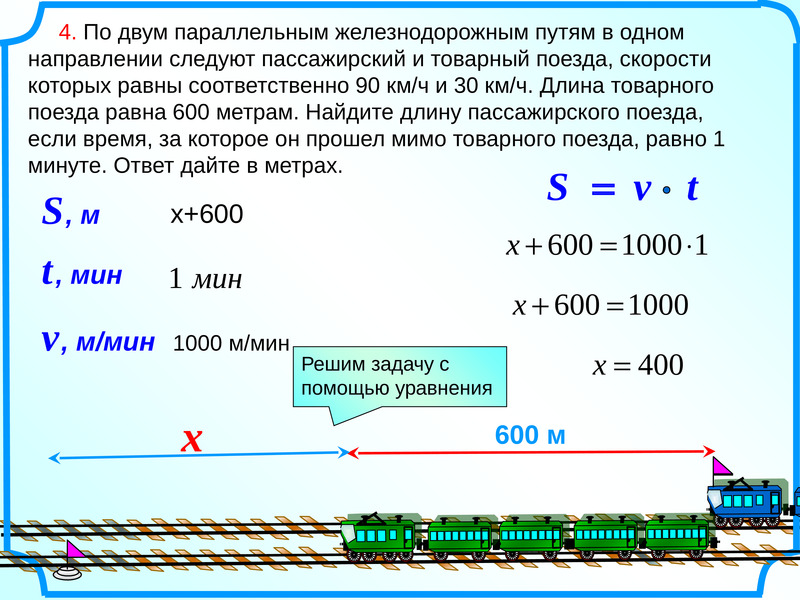 Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704: 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет скорости московского поезда. На каком расстоянии от Ростова встретятся поезда?
Решение
Найдем скорость ростовского поезда. Она составляет скорости московского поезда. Поэтому чтобы определить скорость ростовского поезда, нужно найти от 63 км
63: 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230: 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
Задача 14.
Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Итак, допустим, наши тела двигаются в одном направлении. Как ты думаешь, сколько случаев может быть для такого условия? Правильно, два.
Почему так получается? Уверена, что после всех примеров ты с легкостью сам разберешься, как вывести данные формулы.
Разобрался? Молодец! Пришло время решить задачу.
Четвертая задача
Коля едет на работу на машине со скоростью км/ч. Коллега Коли Вова едет со скоростью км/ч. Коля от Вовы живет на расстоянии км.
Через сколько времени Вова догонит Колю, если из дома они выехали одновременно?
Посчитал? Сравним ответы — у меня получилось, что Вова догонит Колю через часа или через минут.
Сравним наши решения…
Рисунок выглядит вот таким образом:
Похож на твой? Молодец!
Так как в задаче спрашивается, через сколько ребята встретились, а выехали они одновременно, то время, которое они ехали, будет одинаковым, так же как место встречи (на рисунке оно обозначено точкой). Составляя уравнения, возьмем время за.
Составляя уравнения, возьмем время за.
Итак, Вова до места встречи проделал путь. Коля до места встречи проделал путь. Это понятно. Теперь разбираемся с осью передвижения.
Начнем с пути, который проделал Коля. Его путь () на рисунке изображен как отрезок. А из чего состоит путь Вовы ()? Правильно, из суммы отрезков и, где — изначальное расстояние между ребятами, а равен пути, который проделал Коля.
Исходя из этих выводов, получаем уравнение:
Разобрался? Если нет, просто прочти это уравнение еще раз и посмотри на точки, отмеченные на оси. Рисунок помогает, не правда ли?
часа или минут минут.
Надеюсь, на этом примере ты понял, насколько важную роль играет грамотно составленный рисунок!
А мы плавно переходим, точнее, уже перешли к следующему пункту нашего алгоритма — приведение всех величин к одинаковой размерности.
Правило трех «Р» — размерность, разумность, расчет.
Размерность.
Далеко не всегда в задачах дается одинаковая размерность для каждого участника движения (как это было в наших легких задачках).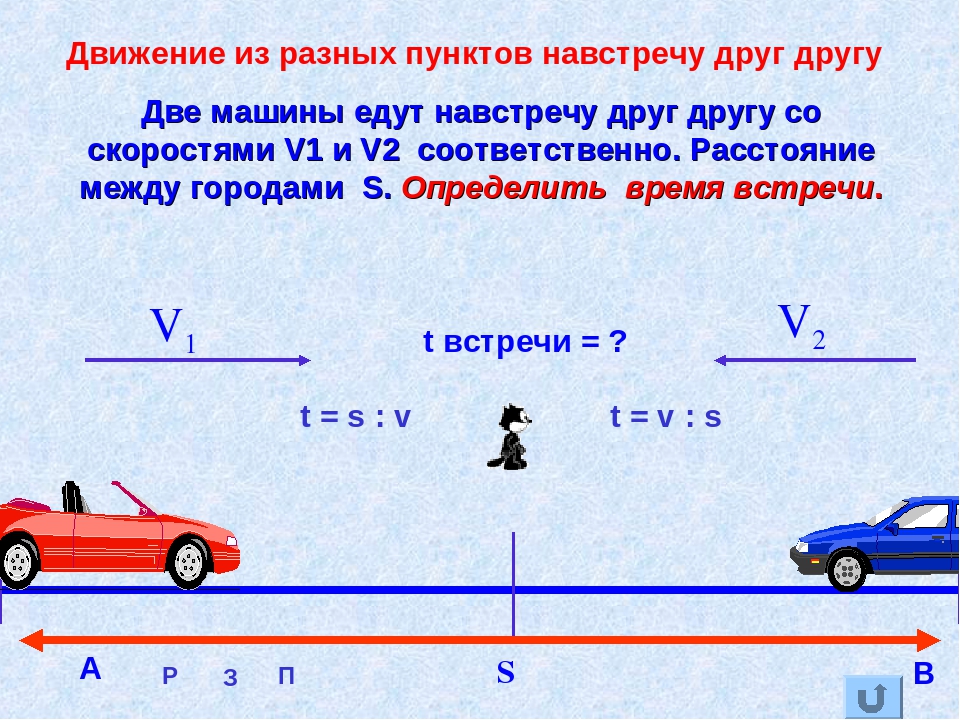
Например, можно встретить задачи, где сказано, что тела двигались определенное количество минут, а скорость их передвижения указана в км/ч.
Мы не можем просто взять и подставить значения в формулу — ответ получится неверный. Даже по единицам измерения наш ответ «не пройдет» проверку на разумность. Сравни:
Видишь? При грамотном перемножении у нас также сокращаются единицы измерения, и, соответственно, получается разумный и верный результат.
А что происходит, если мы не переводим в одну систему измерения? Странная размерность у ответа и % неверный результат.
Итак, напомню тебе на всякий случай значения основных единиц измерения длины и времени.
сантиметр = миллиметров
дециметр = сантиметров = миллиметров
метр = дециметров = сантиметров = миллиметров
километр = метров
минута = секунд
час = минут = секунд
сутки = часа = минут = секунд
Совет: Переводя единицы измерения, связанные с временем (минуты в часы, часы в секунды и т. д.) представь в голове циферблат часов. Невооруженным глазом видно, что минут это четверть циферблата, т.е. часа, минут это треть циферблата, т.е. часа, а минута это часа.
д.) представь в голове циферблат часов. Невооруженным глазом видно, что минут это четверть циферблата, т.е. часа, минут это треть циферблата, т.е. часа, а минута это часа.
А теперь совсем простенькая задача:
Маша ехала на велосипеде из дома в деревню со скоростью км/ч на протяжении минут. Какое расстояние между машиным домом и деревней?
Посчитал? Правильный ответ — км.
минут — это час, и еще минут от часа (мысленно представил себе циферблат часов, и сказал, что минут — четверть часа), соответственно — мин = ч.
Разумность.Ты же понимаешь, что скорость машины не может быть км/ч, если речь, конечно, идет не о спортивном болиде? И уж тем более, она не может быть отрицательной, верно? Так вот, разумность, это об этом)
Расчет.Посмотри, «проходит» ли твое решение на размерность и разумность, и только потом проверяй расчеты. Логично же — если с размерностью и разумностью получается несостыковочка, то проще все зачеркнуть и начать искать логические и математические ошибки.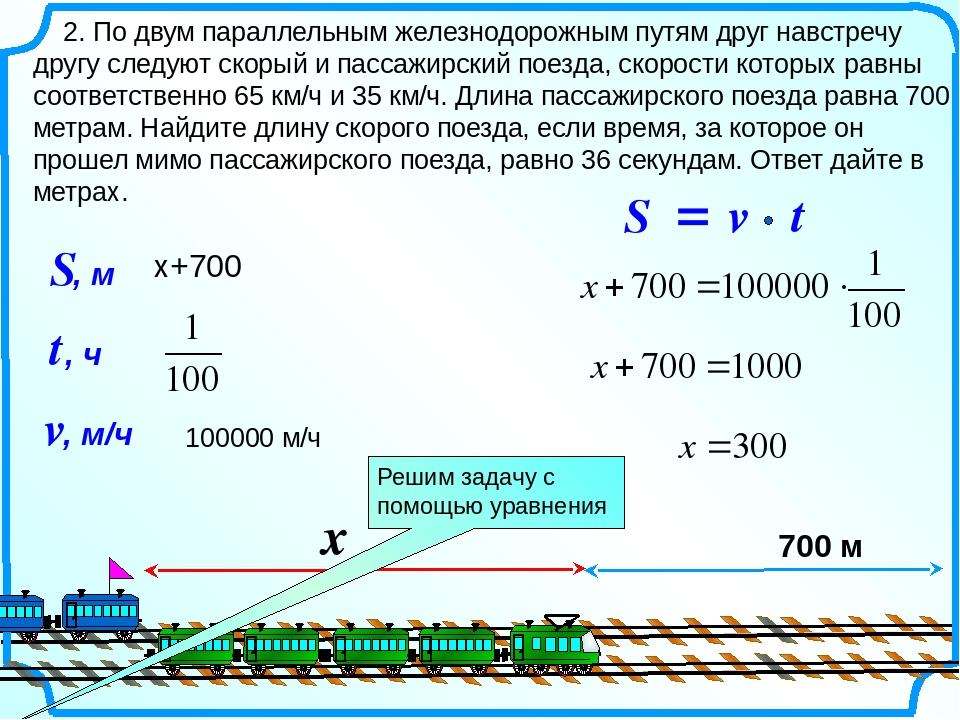
Далеко не всегда задачи на движение такие простые, как мы решали раньше. Очень часто, для того, чтобы правильно решить задачу, нужно не просто нарисовать грамотный рисунок, но и составить таблицу со всеми данными нам условиями.
Первая задача
Из пункта в пункт, расстояние между которыми км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на км больше, чем велосипедист.
Определите скорость велосипедиста, если известно, что он прибыл в пункт на минут позже, чем мотоциклист.
Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать — прямая, пункт, пункт, две стрелочки…
В общем рисуй, и сейчас сравним, что у тебя получилось.
Пустовато как-то, правда? Рисуем таблицу.
Как ты помнишь, все задачи на движения состоят из компонентов: скорость, время и путь . Именно из этих граф и будет состоять любая таблица в подобных задачах.
Правда, мы добавим еще один столбец — имя , про кого мы пишем информацию — мотоциклист и велосипедист.
Так же в шапке укажи размерность , в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?
У тебя получилась вот такая таблица?
Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.
Первое, что мы имеем — это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен км. Вносим!
Возьмем скорость велосипедиста за, тогда скорость мотоциклиста будет …
Если с такой переменной решение задачи не пойдет — ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!
Таблица преобразилась. У нас осталась не заполнена только одна графа — время. Как найти время, когда есть путь и скорость?
Правильно, разделить путь на скорость. Вноси это в таблицу.
Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.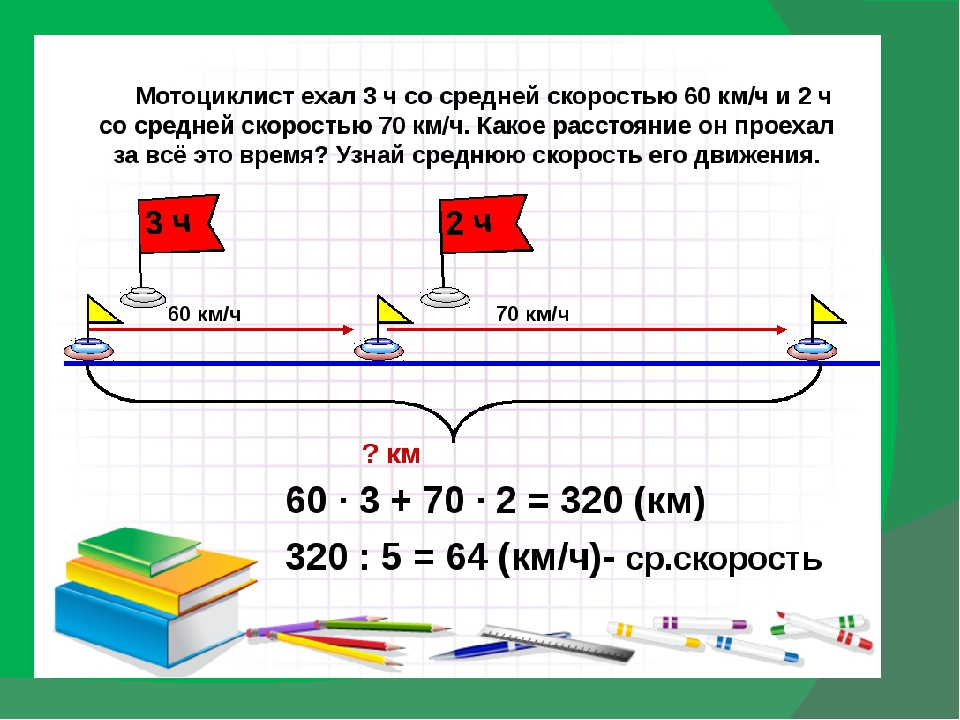
Что мы можем на нем отразить?
Молодец. Скорость передвижения мотоциклиста и велосипедиста.
Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.
Какие данные не отражены ни в таблице, ни на рисунке?
Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени — минут.
Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.
Магия формул: составление и решение уравнений — манипуляции, приводящие к единственно верному ответу.
Итак, как ты уже догадался, сейчас мы будем составлять уравнение .
Составление уравнения:
Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?
Правильно. Мы можем составить уравнение, основываясь на разнице во времени!
Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.
Это уравнение — рациональное. Если не знаешь, что это такое, прочти тему « ».
Приводим слагаемые к общему знаменателю:
Раскроем скобки и приведем подобные слагаемые:Уф! Усвоил? Попробуй свои силы на следующей задаче.
Решение уравнения:
Из этого уравнения мы получаем следующее:
Раскроем скобки и перенесем все в левую часть уравнения:
Вуаля! У нас простое квадратное уравнение. Решаем!
Мы получили два варианта ответа. Смотрим, что мы взяли за? Правильно, скорость велосипедиста.
Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ — км/ч.
Вторая задача
Два велосипедиста одновременно отправились в -километровый пробег. Первый ехал со скоростью, на км/ч большей, чем скорость второго, и прибыл к финишу на часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Напоминаю алгоритм решения:
- Прочитай задачу пару раз — усвой все-все детали.
 Усвоил?
Усвоил? - Начинай рисовать рисунок — в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
- Проверь, все ли величины у тебя одинаковой размерности и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь какие там графы?).
- Пока все это пишешь, думай, что взять за? Выбрал? Записывай в таблицу! Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок — помни о «3Р»!
- Все сделал? Молодец! У меня получилось, что скорость велосипедиста — км/ч.
-«Какого цвета твоя машина?» — «Она красивая!» Правильные ответы на поставленные вопросы
Продолжим наш разговор. Так какая там скорость у первого велосипедиста? км/ч? Очень надеюсь, что ты сейчас не киваешь утвердительно!
Внимательно прочти вопрос: «Какая скорость у первого велосипедиста?»
Понял, о чем я?
Именно! Полученный — это не всегда ответ на поставленный вопрос!
Вдумчиво читай вопросы — возможно, после нахождения тебе нужно будет произвести еще некоторые манипуляции, например, прибавить км/ч, как в нашей задаче.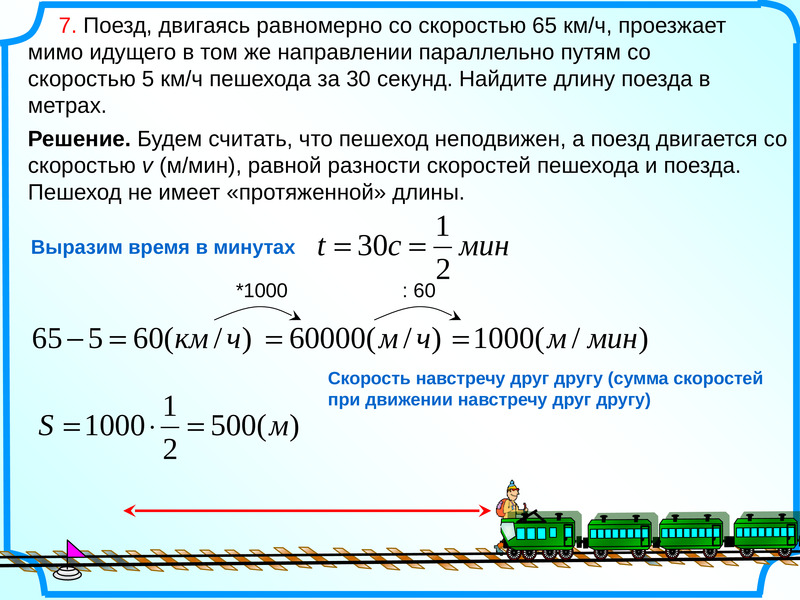
Еще один момент — часто в задачах все указывается в часах, а ответ просят выразить в минутах, или же все данные даны в км, а ответ просят записать в метрах.
Смотри за размерностью не только в ходе самого решения, но и когда записываешь ответы.
Задачи на движение по кругу
Тела в задачах могут двигаться не обязательно прямо, но и по кругу, например, велосипедисты могут ехать по круговой трассе. Разберем такую задачу.
Задача №1
Из пункта круговой трассы выехал велосипедист. Через минут он еще не вернулся в пункт и из пункта следом за ним отправился мотоциклист. Через минут после отправления он догнал велосипедиста в первый раз, а еще через минут после этого догнал его во второй раз.
Найдите скорость велосипедиста, если длина трассы равна км. Ответ дайте в км/ч.
Решение задачи №1
Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:
Между встречами велосипедист проехал расстояние, а мотоциклист — .
Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили — спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.
Разобрался? Попробуй решить самостоятельно следующие задачи:
Задачи для самостоятельной работы:
- Два мо-то-цик-ли-ста стар-ту-ют од-но-вре-мен-но в одном на-прав-ле-нии из двух диа-мет-раль-но про-ти-во-по-лож-ных точек кру-го-вой трас-сы, длина ко-то-рой равна км. Через сколь-ко минут мо-то-цик-ли-сты по-рав-ня-ют-ся в пер-вый раз, если ско-рость од-но-го из них на км/ч боль-ше скорости дру-го-го?
- Из одной точки кру-го-вой трас-сы, длина ко-то-рой равна км, од-н-времен-но в одном на-прав-ле-нии стар-то-ва-ли два мотоциклиста. Ско-рость пер-во-го мотоцикла равна км/ч, и через минут после стар-та он опе-ре-дил вто-рой мотоцикл на один круг. Най-ди-те ско-рость вто-ро-го мотоцикла.
 Ответ дайте в км/ч.
Ответ дайте в км/ч.
- Пусть км/ч — ско-рость пер-во-го мо-то-цик-ли-ста, тогда ско-рость вто-ро-го мо-то-цик-ли-ста равна км/ч. Пусть пер-вый раз мо-то-цик-ли-сты по-рав-ня-ют-ся через часов. Для того, чтобы мо-то-цик-ли-сты по-рав-ня-лись, более быст-рый дол-жен пре-одо-леть из-на-чаль-но раз-де-ля-ю-щее их рас-сто-я-ние, рав-ное по-ло-ви-не длины трас-сы.
Получаем, что время равно часа = минут.
- Пусть ско-рость вто-ро-го мотоцикла равна км/ч. За часа пер-вый мотоцикл про-шел на км боль-ше, чем вто-рой, соответственно, получаем уравнение:
Скорость второго мотоциклиста равна км/ч.
Задачи на течение
Теперь, когда ты отлично решаешь задачи «на суше», перейдем в воду, и рассмотрим страаашные задачи, связанные с течением.
Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, — это стоячая вода.
Скорость течения в озере равна .
Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь — налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести. Это понятно? Логично же.
А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…
Это происходит потому что у реки есть скорость течения , которая относит твой плот по направлению течения.
Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) — он движется со скоростью течения.
Разобрался?
Тогда ответь вот на какой вопрос — «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?
Здесь возможно два варианта.
1-й вариант — ты плывешь по течению.
И тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.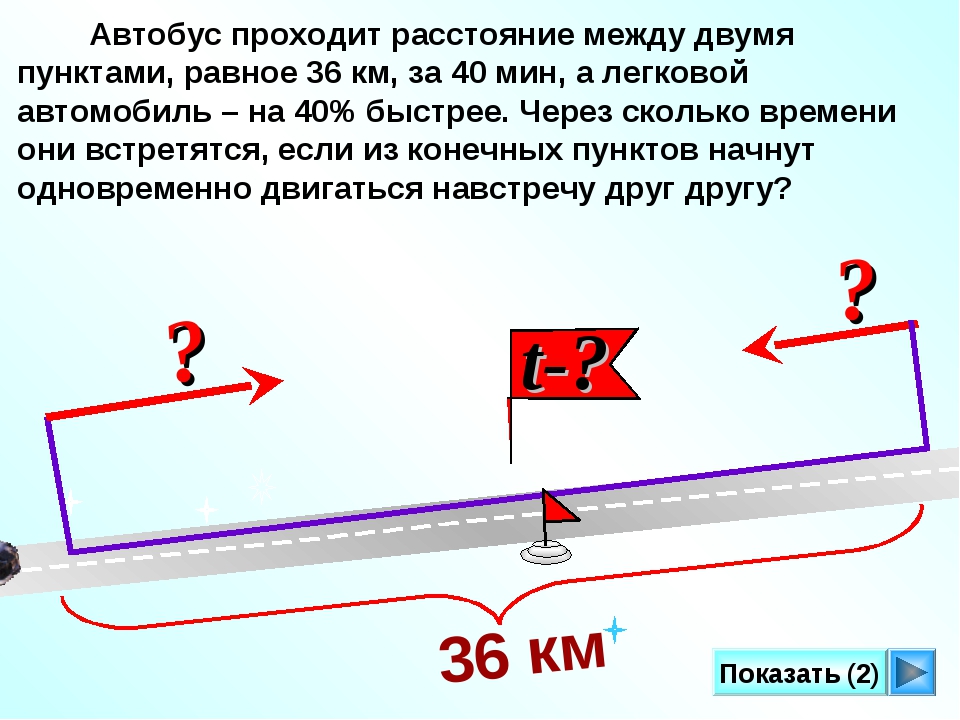
2-й вариант — ты плывешь против течения.
Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость — скорость течения.
Допустим, тебе надо проплыть км. Когда ты преодолеешь это расстояние быстрее? Когда ты будешь двигаться по течению или против?
Решим задачку и проверим.
Добавим к нашему пути данные о скорости течения — км/ч и о собственной скорости плота — км/ч. Какое время ты затратишь, двигаясь по течению и против него?
Конечно, ты без труда справился с этой задачей! По течению — час, а против течения аж часа!
В этом и есть вся суть задач на движение с течением .
Несколько усложним задачу.
Задача №1
Лодка с моторчиком плыла из пункта в пункт часа, а обратно — часа.
Найдите скорость течения, если скорость лодки в стоячей воде — км/ч
Решение задачи №1
Обозначим расстояние между пунктами, как, а скорость течения — как.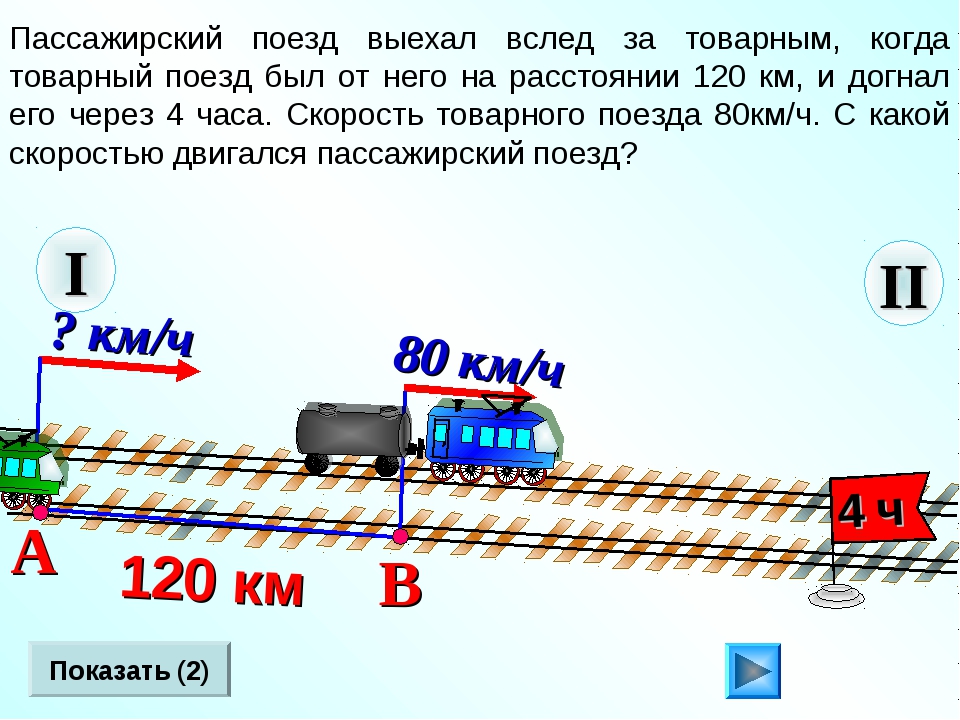
| Путь S | Скорость v, км/ч | Время t, часов | |
| A -> B (против течения) | 3 | ||
| B -> A (по течению) | 2 |
Мы видим, что лодка проделывает один и тот же путь, соответственно:
Что мы брали за?
Скорость течения. Тогда это и будет являться ответом:)
Скорость течения равна км/ч.
Задача №2
Байдарка в вышла из пункта в пункт, расположенный в км от. Пробыв в пункте час минут, байдарка отправилась назад и вернулась в пункт в.
Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки км/ч.
Решение задачи №2
Итак, приступим. Прочитай задачу несколько раз и сделай рисунок. Думаю, ты без труда сможешь решить это самостоятельно.
Все величины у нас выражены в одном виде? Нет. Время отдыха у нас указано и в часах, и в минутах.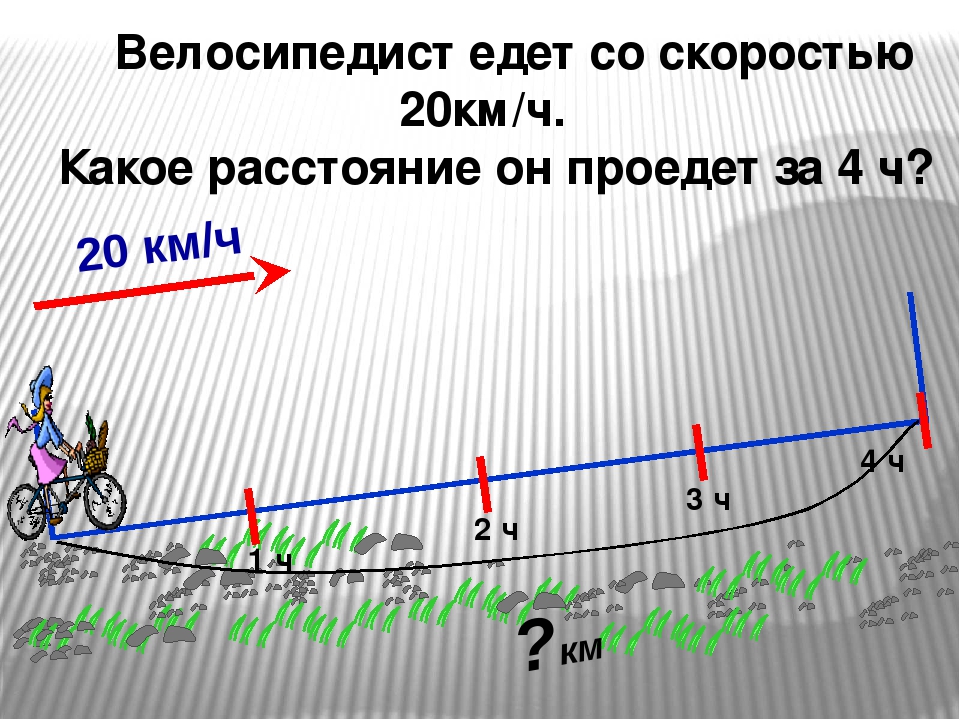
Переведем это в часы:
час минут = ч.
Теперь все величины у нас выражены в одном виде. Приступим к заполнению таблицы и поиску того, что мы возьмем за.
Пусть — собственная скорость байдарки. Тогда, скорость байдарки по течению равна, а против течения равна.
Запишем эти данные, а так же путь (он, как ты понимаешь, одинаков) и время, выраженное через путь и скорость, в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов | |
| Против течения | 26 | ||
| По течению | 26 |
Посчитаем, сколько времени байдарка затратила на свое путешествие:
Все ли часов она плыла? Перечитываем задачу.
Нет, не все. У нее был отдых час минут, соответственно, из часов мы вычитаем время отдыха, которое, мы уже перевели в часы:
ч байдарка действительно плыла.
Приведем все слагаемые к общему знаменателю:
Раскроем скобки и приведем подобные слагаемые. Далее решаем получившееся квадратное уравнение.
Далее решаем получившееся квадратное уравнение.
С этим, я думаю, ты тоже справишься самостоятельно. Какой ответ у тебя получился? У меня км/ч.
Подведем итоги
ПРОДВИНУТЫЙ УРОВЕНЬ
Задачи на движение. Примеры
Рассмотрим примеры с решениями для каждого типа задач.
Движение с течением
Одни из самых простых задач — задачи на движение по реке . Вся их суть в следующем:
- если движемся по течению, к нашей скорости прибавляется скорость течения;
- если движемся против течения, из нашей скорости вычитается скорость течения.
Пример №1:
Катер плыл из пункта A в пункт B часов а обратно — часа. Найдите скорость течения, если скорость катера в стоячей воде км/ч.
Решение №1:
Обозначим расстояние между пунктами, как AB, а скорость течения — как.
Все данные из условия занесем в таблицу:
| Путь S | Скорость v, км/ч | Время t, часов | |
| A -> B (против течения) | AB | 50-x | 5 |
| B -> A (по течению) | AB | 50+x | 3 |
Для каждой строки этой таблицы нужно записать формулу:
На самом деле, можно не писать уравнения для каждой из строк таблицы. Мы ведь видим, что расстояние, пройденное катером туда и обратно одинаково.
Мы ведь видим, что расстояние, пройденное катером туда и обратно одинаково.
Значит, расстояние мы можем приравнять. Для этого используем сразу формулу для расстояния:
Часто приходится использовать и формулу для времени:
Пример №2:
Против течения лодка проплывает расстояние в км на час дольше, чем по течению. Найдите скорость лодки в стоячей воде, если скорость течения равна км/ч.
Решение №2:
Попробуем сразу составить уравнение. Время против течения на час больше, чем время по течению.
Это записывается так:
Теперь вместо каждого времени подставим формулу:
Получили обычное рациональное уравнение, решим его:
Очевидно, что скорость не может быть отрицательным числом, значит, ответ: км/ч.
Относительное движение
Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:
- сумме скоростей, если тела движутся навстречу друг другу;
- разности скоростей, если тела движутся в одном направлении.

Пример №1
Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями км/ч и км/ч. Через сколько минут они встретятся. Если расстояние между пунктами км?
I способ решения:
Относительная скорость автомобилей км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью км/ч. Так как между автомобилями изначально расстояние км, время, через которое второй автомобиль проедет мимо первого:
II способ решения:
Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его. Тогда первый автомобиль проехал путь, а второй — .
В сумме они проехали все км. Значит,
Другие задачи на движение
Пример №1:
Из пункта А в пункт В выехал автомобиль. Одновременно с ним выехал другой автомобиль, который ровно половину пути ехал со скоростью на км/ч меньшей, чем первый, а вторую половину пути он проехал со скоростью км/ч.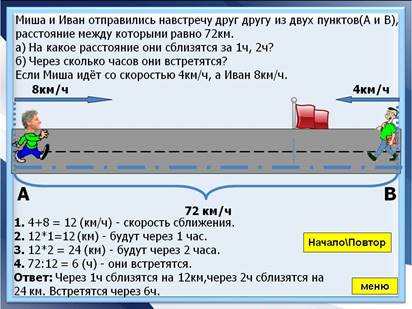
В результате автомобили прибыли в пункт В одновременно.
Найдите скорость первого автомобиля, если известно, что она больше км/ч.
Решение №1:
Слева от знака равно запишем время первого автомобиля, а справа — второго:
Упростим выражение в правой части:
Поделим каждое слагаемое на АВ:
Получилось обычное рациональное уравнение. Решив его, получим два корня:
Из них только один больше.
Ответ: км/ч.
Пример №2
Из пункта A круговой трассы выехал велосипедист. Через минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через минут после отправления он догнал велосипедиста в первый раз, а еще через минут после этого догнал его во второй раз. Найдите скорость велосипедиста, если длина трассы равна км. Ответ дайте в км/ч.
Решение:
Здесь будем приравнивать расстояние.
Пусть скорость велосипедиста будет, а мотоциклиста — . До момента первой встречи велосипедист был в пути минут, а мотоциклист — .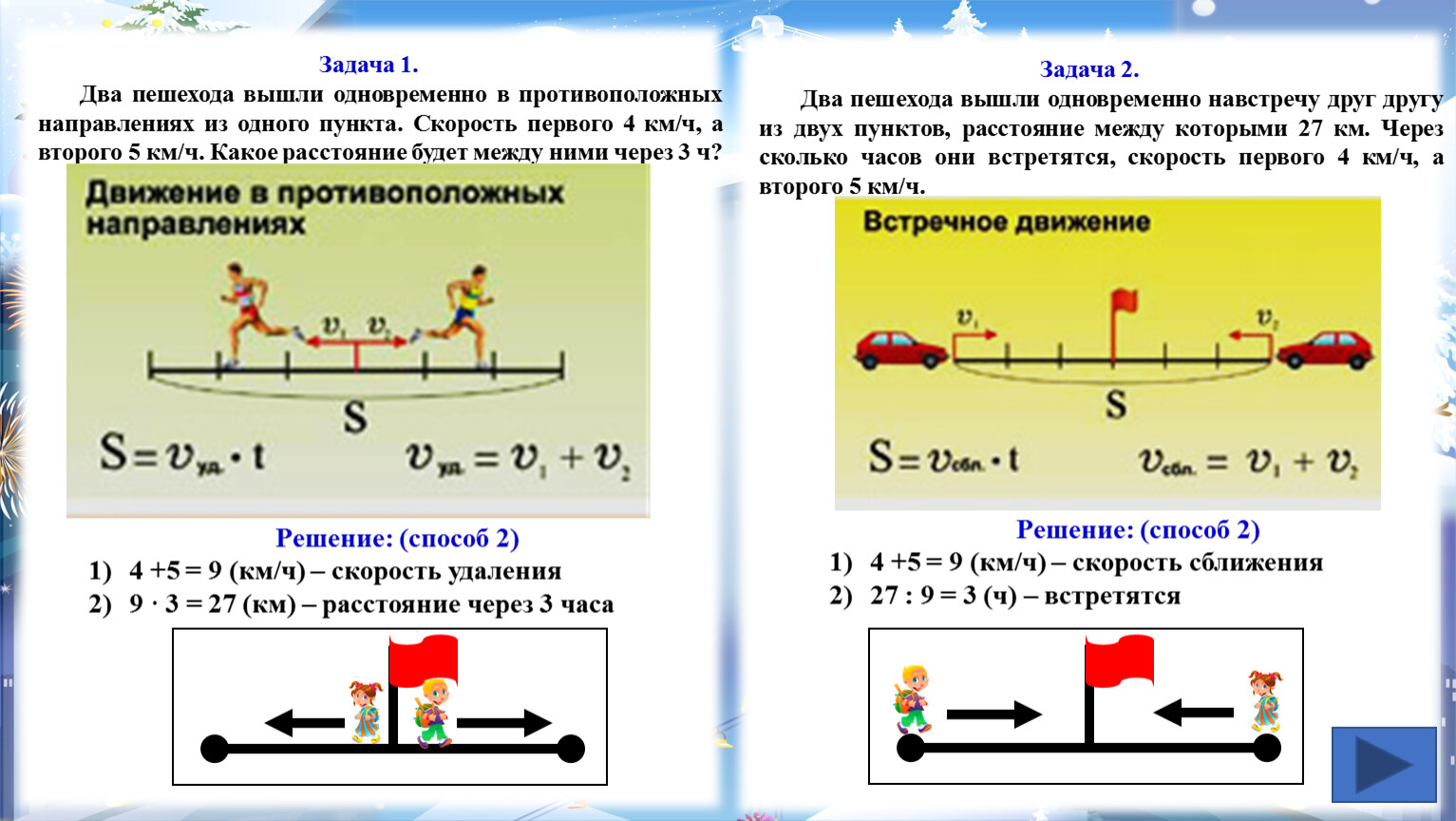
При этом они проехали равные расстояния:
Между встречами велосипедист проехал расстояние, а мотоциклист — . Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили- спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.
Полученные уравнения решаем в системе:
КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
1. Основная формула
2. Относительное движение
- Это сумма скоростей, если тела движутся навстречу друг другу;
- разность скоростей, если тела движутся в одном направлении.
3. Движение с течением :
- Если движемся по течению, к нашей скорости прибавляется скорость течения;
- если движемся против течения, из скорости вычитается скорость течения.
Мы помогли тебе разобраться с задачами на движение…
Теперь твой ход…Если ты внимательно прочитал текст и прорешал самостоятельно все примеры, готовы спорить, что ты все понял.
И это уже половина пути.
Напиши внизу в комментариях разобрался ли ты с задачами на движение?
Какие вызывают наибольшие трудности?
Понимаешь ли ты, что задачи на «работу» — это почти тоже самое?
Напиши нам и удачи на экзаменах!
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Дидактические:
- познакомить с понятиями “скорость сближения”” и “скорость удаления” умения проверять правильность вычислений;
- закрепить умение читать и строить модели движения;
- развивать и закрепить умение решать задачи на движение, умение составлять обратные задачи;
- закрепить вычислительные навыки сложения, вычитания, умножения и деления чисел, а также навыки вычислительных действий с дробями;
Развивающие:
- развитие творческих способностей, памяти, умения мыслить логически грамотно;
- развитие математической грамотной речи;
Воспитательные: воспитание интереса к математике;
Оборудование: Учебник Л. Г. Петерсон “Математика 4 класс, ч.2”,
тестовые карточки. Компьютер, проектор, интерактивная доска. Иллюстративный
материал (презентация в формате MS PowerPoint)
.
Г. Петерсон “Математика 4 класс, ч.2”,
тестовые карточки. Компьютер, проектор, интерактивная доска. Иллюстративный
материал (презентация в формате MS PowerPoint)
.
Ход урока
Организационный момент.
– Здравствуйте, ребята, садитесь! Проверьте, все ли у вас готово к уроку.
– Вспомним правила посадки.
– Запишите число.
Цель урока (Постановка учебной задачи).
– Вспомните, пожалуйста, сколько объектов может одновременно двигаться по
числовому лучу? Откуда могут начинать свое движение объекты? В каких
направлениях могут двигаться объекты? С какой скоростью могут двигаться объекты?
– Сегодня мы выясним, что такое “скорость сближения”, “скорость удаления”, что
нужно знать, чтобы определить, какая это скорость, как найти скорость сближения
или удаления.
– Запишем тему урока “Скорость сближения и скорость удаления”.
Математический диктант.
- Уменьшаемое 130, вычитаемое 111. Найдите разность.
- Делимое 480, делитель 40.
 Найдите частное.
Найдите частное. - На сколько 200 >, чем 184?
- Чему равны 2/3 от числа 27?
- Во сколько раз 320 больше, чем 20?
- Какое число увеличили в 3 раза и получили 57?
- Сумму 95 и 105 разделить на 10.
- 2/5 числа составляют 12. Найдите целое число.
Индивидуальные задания.
Выполняются на доске 2-мя учащимися во время математического диктанта.
Задание 1.
| S | V | t | Формула | |
| I | ? км | 45 км/ч | 7 ч | |
| II | 180 м | ? м/мин | 5 мин | |
| III | 960 м | 16 м/с | ? с | |
| IV | ? км | 60 км/ч | 60 мин |
Задание 2.
Изобразите движение точек на координатном луче и запишите формулу движения точек:
- Движение точки А начинается из точки с координатой (6) в правом направлении со скоростью 3 единичных отрезка в час. Движение точки Б начинается из точки с координатой (14) в левом направлении со скоростью 1 единичный отрезок в час. Чему равны координаты этих точек через 1 час, 2 часа?
- Движение точки А начинается из точки с координатой (6) в левом направлении со скоростью 3 единичных отрезка в час. Движение точки Б начинается из точки с координатой (14) в правом направлении со скоростью 1 единичный отрезок в час. Чему равны координаты этих точек через 1 час, 2 часа?
Проверка математического диктанта и индивидуальных заданий.
Проверка математического диктанта.
– В ответах математического диктанта зашифровано слово. Чтобы расшифровать
его, нам поможет алфавит русского языка.
– Каждый ответ соответствует порядковому номеру буквы в алфавите. Выпишите буквы
в строчку.
Выпишите буквы
в строчку.
Переход на Слайд 2 “Математический диктант”.
– Что у вас получилось? Проверяем.
По каждому клику на Слайде 2 заполняется один столбец таблицы.
– У кого получилось слово “скорость”, ставит себе 5.
– На какие 2 группы можно разделить числа математического диктанта?
- на четные / нечетные
- на круглые / некруглые;
– Что такое “скорость движения”?
Проверка задания 1.
| S | V | t | Формула | |
| I | 315 км | 45 км/ч | 7 ч | S=V*t |
| II | 180 м | 36 м/мин | 5 мин | V=S:t |
| III | 960 м | 16 м/с | 6 с | t=S:V |
| IV | 60 км | 60 км/ч | 60 мин | S=V*t |
– Как найти расстояние, зная скорость и время объекта?
– Как найти скорость, зная расстояние и время объекта?
– Как найти время, зная расстояние и скорость объекта?
Проверка задания 2.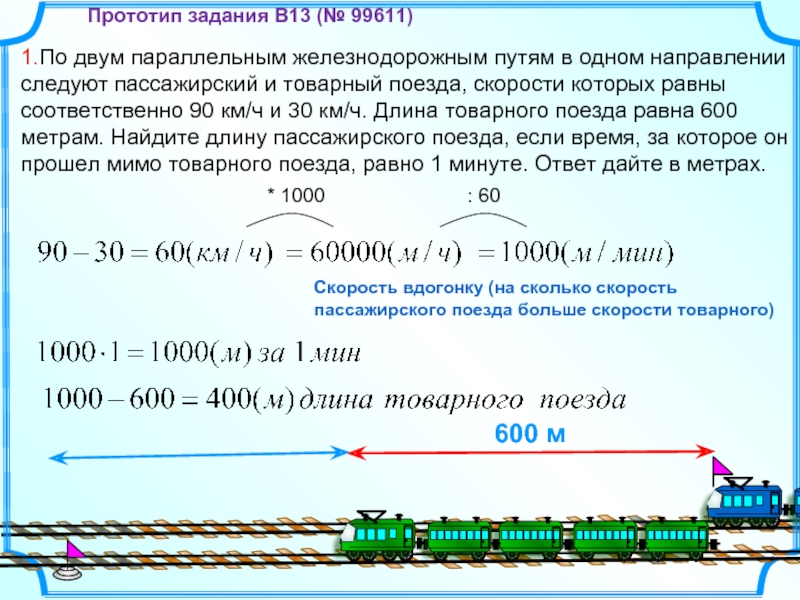
– Сравните 2 чертежа. Что заметили? В чем отличие? Одинаковы ли виды
скоростей?
– Как вы думаете, на каком чертеже будет идти речь о скорости сближения, а где –
о скорости удаления?
Физкультминутка для глаз.
Объяснение понятий “скорость сближения” и “скорость удаления”.
Работа с упражнением 1 урока 24 (Слайды 3–6). По ходу объяснения ученикам задаются вопросы о том, что они видят на экране и после их ответов ученик заполняет таблицу на доске, остальные — в учебниках, затем учитель переходит к следующему шагу анимации.
Переход на Слайд 3 “1) Встречное движение”.
– Посмотрите на экран.
– Что вы можете сказать о движении Мальвины и Буратино?
– Какое это движение?
– В какой точке оказались Мальвина и Буратино через 1 минуту, через 2 минуты,
через 3 минуты? Заполним таблицу.
– Сделаем вывод.
Переход на Слайд 4 “2) Движение в противоположных направлениях”.
– Посмотрите на экран.
– Что вы можете сказать о движении Синьора Помидора и Чиполлино?
– Какое это движение? Заполним таблицу.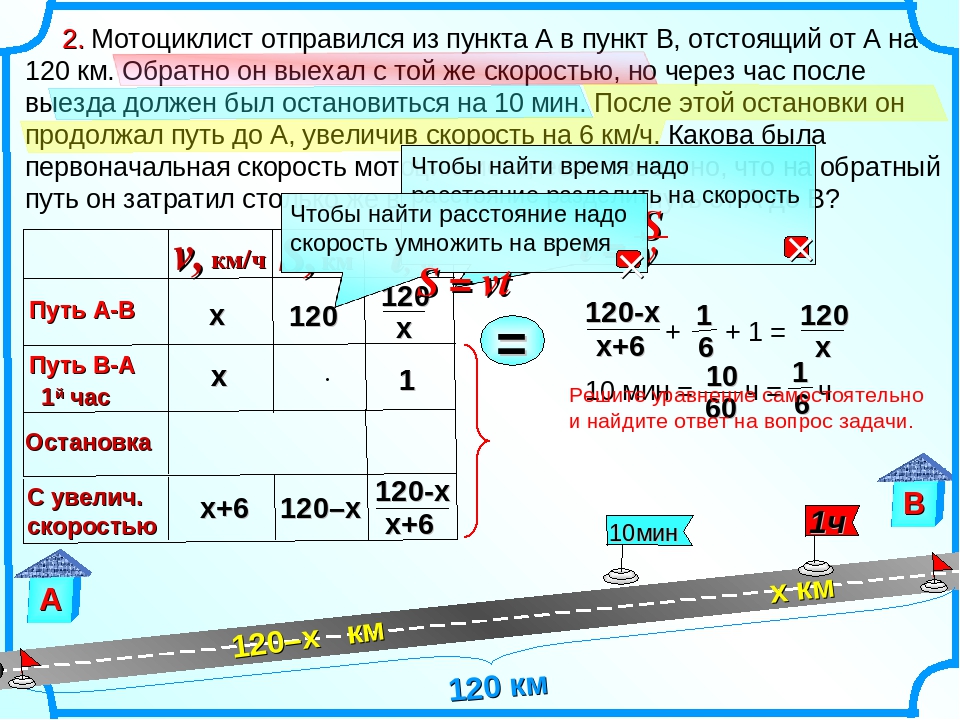
– Из каких точек началось их движение? Заполним таблицу.
– В какой точке оказались Синьор Помидор и Чиполлино через 1 минуту, через 2
минуты, через 3 минуты? Заполним таблицу.
– Что происходит с расстоянием между объектами?
– Произойдет ли встреча?
– Сделаем вывод.
Переход на Слайд 5 “3) Движение вдогонку”.
– Посмотрите на экран.
– Что вы можете сказать о движении Крокодила Гены и Чебурашки?
– Какое это движение?
– Из каких точек началось их движение? Заполним таблицу.
– В какой точке оказались Крокодил Гена и Чебурашка через 1 минуту, через 2
минуты, через 3 минуты? Заполним таблицу.
– На сколько уменьшается расстояние между ними через каждую минуту?
– В какой точке и через сколько минут произошла встреча?
– Сделаем вывод.
Переход на Слайд 6 “4) Движение с отставанием””.
– Посмотрите на экран
– Что вы можете сказать о движении Пончика и Незнайки?
– Какое это движение?
– Из каких точек началось их движение?
– В какой точке оказались Пончик и Незнайка через 1 минуту, через 2 минуты,
через 3 минуты? Заполним таблицу.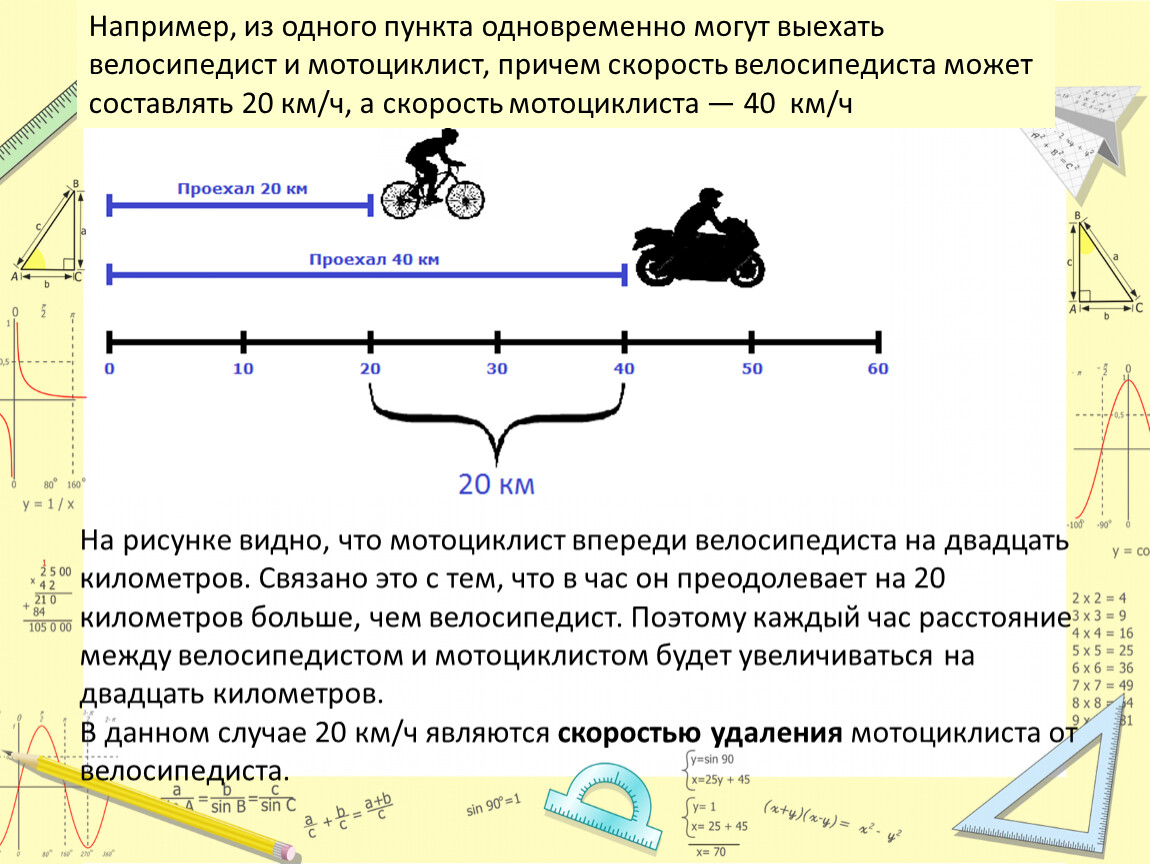
– Что происходит с расстоянием между объектами? Почему?
– На сколько увеличивается расстояние между ними через каждую минуту?
– Произойдет ли встреча?
– Сделаем вывод.
– Что такое “скорость сближения”? (Это расстояние, на которое сближаются
объекты за единицу времени. )
– Что такое “скорость удаления”? (Это расстояние, на которое удаляются
объекты за единицу времени. )
Составление опорной схемы.
Переход на Слайд 7 “Опорная схема”.
– Составим опорные схемы ко всем видам движения.
Физкультминутка.
Мы к лесной лужайке вышли,
Поднимая ноги выше,
Через кустики и кочки,
Через ветви и пенечки.
Кто высоко так шагал –
Не споткнулся, не упал.
Решение задач с комментированием.
Для закрепления знаний учащимися разбираются и решаются задачи на все виды
движения.
– Решим несколько задач и определим, о какой скорости: сближения или
удаления идет речь? Чему она равна? А помогут нам в этом герои сказки “Золотой
ключик”.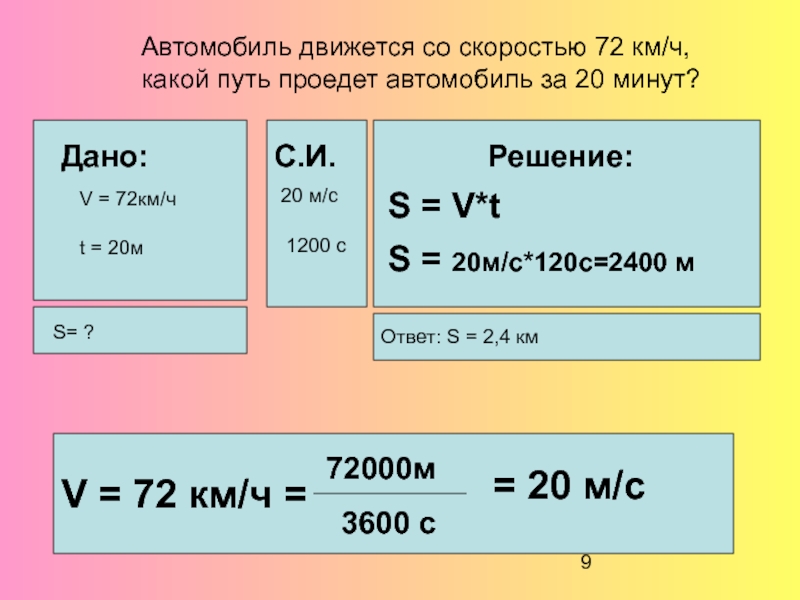
Работа со Слайдами 8–11. Ученики определяют по Слайду, к какой опорной схеме относится задача, и предлагают способ ее решения.
Работа с классом:
- Переход на Слайд 8 “Задача на движение в противоположных направлениях”.
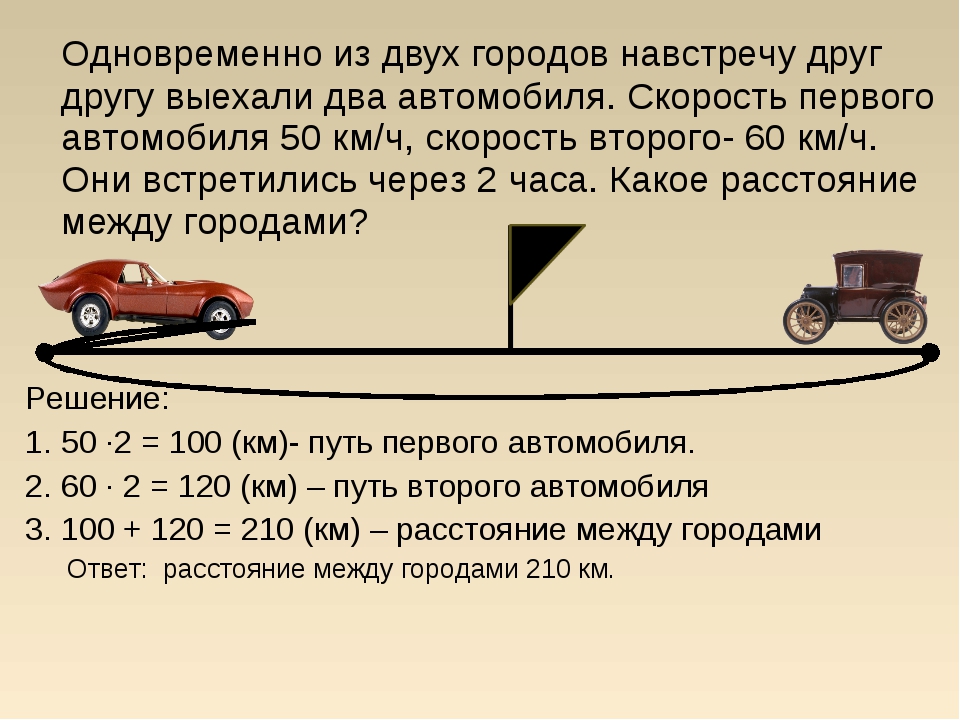
Индивидуально:
- Разбойники гонятся за Буратино, который убегает от них со скоростью 19 ед./мин. Как изменяется расстояние между Буратино и разбойниками, если они бегут со скоростью 23 ед./мин.
- Составьте обратную задачу к 1-ой задаче.
- Измените условие 2-ой задачи так, чтобы она решалась “-”.
- Измените условие 4-ой задачи так, чтобы она решалась “+”.
Самостоятельное решение задач (тест).
Для проверки знаний и умений по данной теме учащиеся получили тестовые
карточки с заданием “Установите соответствие между схемой задачи и ее решением
(1 и 2 варианты)”.
– Рассмотрите схемы задач, определите, о какой скорости движения идет речь
(сближения или удаления), соедините с подходящим выражением и вычислите его.
Взаимопроверка решений задач.
Учащиеся проверяют выполнение задания с помощью Слайдов 12–13.
Итог урока.
– Подошёл к концу наш урок. О чем сегодня узнали на уроке? Что важно знать, чтобы определить скорость сближения или удаления? Что вам особенно понравилось, запомнилось?
Домашнее задание.
Примеры, задача
Выставление отметок и поощрение учеников.
В течение всего урока работа и ответы учеников оценивались словесно и поощрительными медальками.
Список использованных источников и литературы.
- Учебник Л.Г. Петерсон “Математика 4 класс, ч.2”.
- Картинки с персонального сайта Николая Козлова http://nkozlov.ru/library/s318/d3458/
Расстояние, скорость и время
Пройденное расстояние, поддерживаемая средняя скорость и прошедшее время связаны следующим образом:
или, как используется в классах естественных наук
Помните: преобразование единиц времени
Умножьте час на 60, чтобы получить минуты:
1,15 часа означает 1 час 9 минут, а не 1 час 15 минут,
с 0.15 x 60 = 9, а не 15
Разделите минуты на 60, чтобы получить десятичную дробь:
3 часа 45 минут = 3,75 часа, а не 3,45 часа,
поскольку 45/60 = 0,75, а не 0,45
Чтобы преобразовать километры в час в метры в секунду
, так как в километре тысяча метров, в минуте шестьдесят секунд, в часе шестьдесят минут.
Чтобы преобразовать метры в секунду в километры в час
Преобразование миль в километры
Для преобразования километров в мили
или
Пройденное расстояние
Примеры
Человек идет 3 часа со скоростью
3 мили в час.
Как далеко он продвинулся?
Человек идет 45 минут со скоростью
4 мили в час.
Как далеко он продвинулся?
Преобразование минут в часы:
т.
Поддерживается средняя скорость
Примеры
Мужчина преодолевает расстояние в 21 милю в
7 часов.
Рассчитайте его среднюю скорость.
Человек преодолевает расстояние в 232 мили в
7 часов 15 минут.
Какая у него была средняя скорость?
Преобразование минут в часы:
т.
Затраченное время
Примеры
Сколько времени занимает самолет путешествуя со скоростью 580 км в час, чтобы путешествовать расстояние 232 километра?
преобразовать в минуты
Мужчина проехал 250 миль со средней скоростью 70 миль в час.
Сколько времени длилось путешествие ?
Ответьте в часах, минутах и секундах.
преобразовать в минуты
преобразовать в секунды
График перехода на летнее время
© Александр ФоррестСколько времени нужно, чтобы проехать 60 км? — MVOrganizing
Сколько времени нужно, чтобы проехать 60 км?
Однако проще понять, что 60 км / ч означает 1 км каждую минуту.Итак, 5 км / ч означает 5 минут. 30 км займет 30 минут и, конечно же, 60 км займет 60 минут (час).
Сколько времени нужно проехать 50 км?
Для проезда 50 км требуется 0,41667 часа или 25 минут, если вы едете со скоростью 120 километров в час. Travelmath поможет вам определить время вождения на основе фактических направлений вашей поездки.
Сколько времени нужно, чтобы проехать 1 км?
Метод 1. Сначала мы вычисляем, сколько минут нужно, чтобы проехать 1 км на обеих скоростях: 60/100 = это займет 0.6 минут, чтобы проехать 1 км.
Как долго длится поездка 80 км?
80 км за час. 80 км за 60 минут.
Сколько часов езды составляет 30 км?
Время = расстояние / скорость. Таким образом, довольно легко было бы узнать, сколько часов нужно, чтобы преодолеть 30 км, когда вы путешествуете со скоростью 120 км / ч. Время = 30 км / 120 км / ч = 0,25 часа. Если вам нужно выяснить, сколько это минут, просто умножьте это на 60, и вы получите 15 минут.
Какова скорость автомобиля после преодоления расстояния 350 км за 7 часов?
Ответ: Скорость автомобиля 50 км / ч или 50 км / ч.
Сколько часов нужно, чтобы проехать 350 км?
В цифрах это 4,375 часа, или 4 часа 22,5 минуты.
Сколько времени нужно, чтобы проехать 50 км При движении со скоростью 10 км HR a 180 мин C 300 мин B 60 мин D 250 мин?
Это займет 5 часов.
Какая скорость 60 км за 5 часов?
60 км × 5 часов = 300 км.
Какова скорость автомобиля, который преодолевает 52 км за 2 часа?
26 км / ч — вот ответ.
Какая будет скорость тела в метрах в секунду, если оно преодолеет 40 км за 5 часов?
Ответ подтвержден экспертом => Расстояние = 40 км.=> Время (t) = 5 часов. => 8 км / час. 5 часов = 5 × 60 × 60 сек.
Как скорость — это вектор?
Скорость как векторная величина. Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости. Скорость — это векторная величина. Таким образом, скорость учитывает направление.
Как вы будете различать расстояние, пройденное объектом, и его смещение, запишите важные характеристики пройденного расстояния и смещения?
1.Расстояние — это длина пути, пройденного телом при перемещении из исходного положения в конечное; Смещение — это кратчайшее расстояние между исходным положением и конечным положением тела. 2. Расстояние — скалярная величина; Смещение — это векторная величина.
В чем разница между расстоянием и смещением?
Расстояние — это скалярная величина, которая указывает, «сколько земли покрыл объект» во время своего движения. Смещение — это векторная величина, которая указывает, «насколько далеко находится объект»; это общее изменение положения объекта.
Является ли расстояние векторной величиной?
Смещение — это пример векторной величины. Расстояние — это пример скалярной величины. Вектор — это любая величина, имеющая как величину, так и направление.
Работа — это векторная величина?
Также мы знаем, что работа — это скалярное произведение векторов силы и смещения. Поскольку скалярное произведение — это скалярная величина. Итак, работа — это скалярная величина, она имеет только величину, а не направление.
Является ли угловой момент векторной величиной?
Угловой момент — это векторная величина, требующая указания как величины, так и направления для его полного описания.
Как рассчитать расстояние?
Чтобы найти расстояние, используйте формулу для расстояния d = st, или расстояние равно скорости, умноженной на время. Скорость и скорость аналогичны, поскольку они оба представляют собой расстояние в единицу времени, например мили в час или километры в час. Если скорость r такая же, как скорость s, r = s = d / t.
2.2 Скорость и скорость — физика
Задачи обучения раздела
К концу этого раздела вы сможете делать следующее:
- Вычислить среднюю скорость объекта
- Связать смещение и среднюю скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (B) описывают и анализируют движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Кроме того, Руководство лаборатории физики средней школы рассматривает содержание этого раздела лаборатории под названием «Положение и скорость объекта», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (В) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.
Раздел Основные термины
| средняя скорость | средняя скорость | мгновенная скорость |
| мгновенная скорость | скорость | скорость |
Поддержка учителя
Поддержка учителя
В этом разделе учащиеся применяют то, что они узнали о расстоянии и смещении, к понятиям скорости и скорости.
[BL] [OL] Прежде чем студенты прочитают раздел, попросите их привести примеры того, как они слышали слово «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что эти слова часто используются как синонимы в повседневной жизни, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.
[AL] Объясните учащимся, что скорость, как и смещение, является векторной величиной. Попросите их поразмышлять о том, чем скорость отличается от скорости.После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Какой пример? Как можно применить эти термины к движению, которое вы видите каждый день?
Скорость
Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.
Описание того, насколько быстро или медленно движется объект, — это его скорость. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость — это скаляр, потому что у нее есть величина, но не направление. Поскольку скорость — это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала
Единицей времени в СИ является секунда (с), а единицей измерения скорости в системе СИ являются метры в секунду (м / с), но иногда километры в час (км / ч), мили в час (миль / ч) или другие единицы измерения. скорость используются.
Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость v avg — это пройденное расстояние, разделенное на время, в течение которого происходит движение.
vavg = distancetimevavg = distancetimeВы, конечно, можете изменить уравнение для решения либо расстояния, либо времени
время = distancevavg.time = distancevavg. distance = vavg × timedistance = vavg × timeПредположим, что автомобиль проезжает 150 километров за 3 секунды.2 часа. Его средняя скорость за поездку —
. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч.Скорость автомобиля, вероятно, увеличится и уменьшится во много раз за 3,2 часа поездки. Однако его скорость в определенный момент времени — это его мгновенная скорость. Спидометр автомобиля показывает его мгновенную скорость.
Поддержка учителей
Поддержка учителей
[OL] [AL] Предупредите учащихся, что средняя скорость не всегда равна средней начальной и конечной скорости объекта.Например, предположим, что автомобиль проезжает 100 км. Первые 50 км он движется со скоростью 30 км / ч, а вторые 50 км — со скоростью 60 км / ч. Его средняя скорость будет составлять расстояние / (временной интервал) = (100 км) / [(50 км) / (30 км / ч) + (50 км) / (60 км / ч)] = 40 км / ч. Если бы автомобиль на этих скоростях проехал равное время на 30 и 60 км, а не на равные расстояния, его средняя скорость составила бы 45 км / ч.
[BL] [OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» на обыденном языке часто называют просто скоростью.Подчеркните важность использования правильной терминологии в науке, чтобы избежать путаницы и правильно передавать идеи.
Рис. 2.8 За 30 минут до магазина туда и обратно общее расстояние составляет 6 км. Средняя скорость 12 км / ч. Смещение для обхода равно нулю, потому что не было чистого изменения положения.
Рабочий пример
Расчет средней скорости
Мрамор катится 5,2 м за 1,8 с. Какая была средняя скорость мрамора?
Стратегия
Мы знаем расстояние, которое проходит мрамор, 5.2 м, интервал времени 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.
Решение
vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / сОбсуждение
Средняя скорость — это скаляр, поэтому мы не включаем направление в ответ. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды — это 2,5 м / с. Поскольку 2,5 м / с близко к 2,9 м / с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.
Практические задачи
8.Питчер перебрасывает бейсбольный мяч от насыпи питчера к своей тарелке за 0,46 с. Дистанция 18,4 м. Какая была средняя скорость бейсбольного мяча?
- 40 м / с
- -40 м / с
- 0,03 м / с
- 8,5 м / с
Кэсси шла к дому своей подруги со средней скоростью 1,40 м / с. Расстояние между домами 205 м. Как долго она продолжала путешествие?
- 146 с
- 0.01 с
- 2,50 мин
- 287 с
Скорость
Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость — это смещение, деленное на время, в течение которого смещение происходит.
vavg = время смещения = ΔdΔt = df − d0tf − t0vavg = время смещения = ΔdΔt = df − d0tf − t0Скорость, как и скорость, выражается в единицах СИ в метрах в секунду (м / с), но поскольку это вектор, вы также должны включить направление.Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.
Советы для успеха
Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели в предыдущем разделе со смещением и расстоянием, изменение направления во временном интервале больше влияет на скорость и скорость.
Предположим, что пассажир двигался к задней части самолета со средней скоростью –4 м / с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или отступил, прежде чем он добрался до задней части самолета. Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени, такие как те, что показаны на рисунке 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, которая является скоростью в определенный момент времени.Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.
Рис. 2.9. На диаграмме представлена более подробная запись пассажира самолета, направлявшегося к задней части самолета, показаны более мелкие отрезки его полета.
Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой.Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.
Watch Physics
Расчет средней скорости или скорости
В этом видео рассматриваются векторы и скаляры и описывается, как вычислить среднюю скорость и среднюю скорость, когда вы знаете смещение и изменение во времени. В видео также рассказывается, как преобразовать км / ч в м / с.
Проверка захвата
Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
- Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
Поддержка учителей
Поддержка учителей
Это видео хорошо подчеркивает разницу между векторами и скалярами.Студент знакомится с идеей использования «s» для обозначения смещения, которое вы можете поощрять, а можете и не поощрять. Прежде чем ученики посмотрят видео, укажите, что преподаватель использует s → s → для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является обычным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часа и секунды. Напомните учащимся, что в своей работе они должны использовать сокращения h для часа и s для секунд.
Рабочий пример
Расчет средней скорости
Студент перемещается на 304 м к северу за 180 с. Какая была средняя скорость ученика?
Стратегия
Мы знаем, что смещение составляет 304 м к северу, а время — 180 с. Мы можем использовать формулу для средней скорости, чтобы решить задачу.
Решение
vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север2,1
Обсуждение
Поскольку средняя скорость является векторной величиной, вы должны включить в ответ направление и величину.Обратите внимание, однако, что направление можно не указывать до конца, чтобы не загромождать проблему. Обратите внимание на значащие цифры в задаче. Расстояние 304 м состоит из трех значащих цифр, а временной интервал 180 с — только двух, поэтому частное должно состоять только из двух значащих цифр.
Советы для успеха
Обратите внимание на способ представления скаляров и векторов. В этой книге d обозначает расстояние и перемещение. Точно так же v обозначает скорость, а v обозначает скорость.Переменная, не выделенная жирным шрифтом, указывает на скалярную величину, а переменная, выделенная жирным шрифтом, указывает на векторную величину. Иногда векторы представлены маленькими стрелками над переменной.
Поддержка учителей
Поддержка учителей
Используйте эту задачу, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые студенты имеют тенденцию включать много цифр в свои окончательные вычисления. Они ошибочно полагают, что повышают точность своего ответа, записывая многие цифры, указанные на калькуляторе.Обратите внимание, что это приводит к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда использовать одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.
Рабочий пример
Решение для смещения, когда известны средняя скорость и время
Лейла бегает трусцой со средней скоростью 2.4 м / с на восток. Каково ее смещение через 46 секунд?
Стратегия
Мы знаем, что средняя скорость Лейлы составляет 2,4 м / с на восток, а временной интервал составляет 46 секунд. Мы можем изменить формулу средней скорости, чтобы найти смещение.
Решение
vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток2,2
Обсуждение
Ответ: примерно в 110 м к востоку, что является разумным смещением для чуть менее минуты бега трусцой.Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя научную нотацию, потому что мы хотели прояснить, что мы использовали только две значащие цифры.
Советы для успеха
Размерный анализ — хороший способ определить, правильно ли вы решили проблему. Запишите расчет, используя только единицы измерения, чтобы убедиться, что они совпадают на противоположных сторонах отметки равенства. В рассмотренном примере у вас
м = (м / с) (с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица компенсирует, оставляя только m и, конечно же, m = m.
Рабочий пример
Решение для времени, когда известны смещение и средняя скорость
Филипп идет по прямой дорожке от своего дома до школы. Сколько времени ему потребуется, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м / с на запад?
Стратегия
Мы знаем, что смещение Филиппа составляет 428 м к западу, а его средняя скорость составляет 1,7 м / с к западу. Мы можем рассчитать время, необходимое для поездки, переписав уравнение средней скорости.
Решение
vavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 svavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 с2,3
Обсуждение
Здесь нам снова пришлось использовать научную запись, потому что ответ мог состоять только из двух значащих цифр. Поскольку время является скаляром, ответ включает только величину, а не направление.
Практические задачи
10.Дальнобойщик проезжает по прямой трассе 0,25 ч со смещением 16 км к югу.Какова средняя скорость дальнобойщика?
- 4 км / ч север
- 4 км / ч юг
- 64 км / ч север
- 64 км / ч юг
Птица летит со средней скоростью 7,5 м / с на восток от ветки к ветке за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м / с на восток в течение 3,5 с к другому ответвлению. Каково полное смещение птицы от начальной точки?
- 42 м к западу
- 6 м запад
- 6 м на восток
- 42 м на восток
Virtual Physics
The Walking Man
В этом симуляторе вы наведете курсор на человека и переместите его сначала в одном направлении, а затем в противоположном.Не отключайте вкладку Introduction . Вы можете использовать вкладку Charts после того, как узнаете о графическом движении позже в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. Пока не обращайте внимания на поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость — отрицательным. Затем посмотрите, сможете ли вы сделать обратное.
Проверка захвата
Какая ситуация правильно описывает, когда положение движущегося человека было отрицательным, но его скорость была положительной?
- Человек движется к 0 слева от 0
- Человек движется к 0 справа от 0
- Мужчина удаляется от 0 слева от 0
- Мужчина движется от 0 справа от 0
Поддержка учителей
Поддержка учителей
Это мощная интерактивная анимация, которую можно использовать для многих уроков.На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Он также может показать, что при отрицательном смещении скорость может быть как положительной, так и отрицательной. Позже с его помощью можно будет показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется оставить учащихся на вкладке Введение . Вкладку Charts можно использовать после того, как студенты узнают о графическом движении позже в этой главе.
Проверьте свое понимание
12.Два бегуна, идущие по одной прямой, начинают и заканчивают свой бег одновременно. На полпути у них разные мгновенные скорости. Могут ли их средние скорости на протяжении всей поездки быть одинаковыми?
- Да, потому что средняя скорость зависит от чистого или полного смещения.
- Да, потому что средняя скорость зависит от общего пройденного расстояния.
- Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
- Нет, потому что мгновенные скорости бегунов должны оставаться такими же в средней точке, но могут изменяться в других точках.
Если вы разделите общее расстояние, пройденное за поездку на автомобиле (определенное одометром), на время поездки, вычисляете ли вы среднюю скорость или величину средней скорости, и при каких обстоятельствах эти две величины одинаковы? ?
- Средняя скорость. Оба они одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
- Средняя скорость. Оба они одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
- Величина средней скорости. И то, и другое одинаково, когда автомобиль движется с постоянной скоростью.
- Величина средней скорости. И то, и другое одинаково, когда машина не меняет своего направления.
Может ли средняя скорость быть отрицательной?
- Да, если чистое смещение отрицательное.
- Да, если направление объекта меняется во время движения.
- Нет, потому что средняя скорость описывает только величину, а не направление движения.
- Нет, потому что средняя скорость описывает только величину в положительном направлении движения.
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание », чтобы оценить, насколько учащиеся достигли целей обучения по разделам. Если учащиеся не справляются с какой-либо конкретной целью, Check Your Understanding поможет определить, кто из них и направит учащихся к соответствующему содержанию.Тестовые задания в TUTOR позволят вам переоценить.
Проблемы относительной скорости и речных судов
Иногда объекты движутся в среде, которая движется относительно наблюдателя. Например, самолет обычно встречает ветер — воздух, который движется относительно наблюдателя на земле внизу. Другой пример: моторная лодка на реке движется среди речного течения — воды, движущейся по отношению к наблюдателю на суше. В таких случаях, как этот, величина скорости движущегося объекта (будь то самолет или моторная лодка) относительно наблюдателя на суше не будет такой же, как показания спидометра транспортного средства.Другими словами, спидометр на моторной лодке может показывать 20 миль / час; тем не менее, моторная лодка может двигаться относительно наблюдателя на берегу со скоростью 25 миль в час. Движение относительно наблюдателя. Наблюдатель на суше, часто называемый (или ошибочно называемый) «неподвижным наблюдателем», измерял бы скорость, отличную от скорости человека на лодке. Наблюдаемая скорость лодки всегда должна описываться относительно того, кто является наблюдателем.
Попутный ветер, встречный и боковой ветерЧтобы проиллюстрировать этот принцип, рассмотрим самолет, летящий при попутном ветре .Попутный ветер — это просто ветер, который приближается к самолету сзади, увеличивая его результирующую скорость. Если самолет движется со скоростью 100 км / час по отношению к воздуху, и если скорость ветра составляет 25 км / час, то какова скорость самолета относительно наблюдателя на земле внизу? Результирующая скорость самолета (то есть результат влияния скорости ветра на скорость двигателя самолета) представляет собой векторную сумму скорости самолета и скорости ветра.Эту результирующую скорость довольно легко определить, если ветер приближается к самолету прямо сзади. Как показано на схеме ниже, самолет движется со скоростью 125 км / ч относительно земли.
Если самолет встречает встречный ветер, результирующая скорость будет меньше 100 км / ч. Поскольку встречный ветер — это ветер, который приближается к самолету спереди, такой ветер уменьшит результирующую скорость самолета. Предположим, что самолет, летящий со скоростью 100 км / час по отношению к воздуху, встречает встречный ветер со скоростью 25 км / час.В этом случае результирующая скорость будет 75 км / ч; это скорость самолета относительно наблюдателя на земле. Это показано на диаграмме ниже.
Теперь рассмотрим самолет, летящий со скоростью 100 км / час на юг, который встречает боковой ветер 25 км / час на западе. А какова будет результирующая скорость самолета? На этот вопрос можно ответить так же, как и на предыдущие вопросы. Результирующая скорость самолета — это векторная сумма двух отдельных скоростей.Чтобы определить результирующую скорость, к скорости ветра необходимо прибавить плоскую скорость (относительно воздуха). Это та же процедура, которая использовалась выше для ситуаций встречного и попутного ветра; только теперь результат вычислить не так просто. Поскольку два добавляемых вектора — скорость в южной плоскости и скорость западного ветра — расположены под прямым углом друг к другу, можно использовать теорему Пифагора. Это показано на диаграмме ниже.
В этой ситуации бокового ветра вектор, направленный на юг, может быть добавлен к вектору, направленному на запад, с использованием обычных методов сложения векторов.Величина результирующей скорости определяется с помощью теоремы Пифагора. Алгебраические шаги следующие:
(100 км / ч) 2 + (25 км / ч) 2 = 2 рэнд10 000 км 2 / час 2 + 625 км 2 / час 2 = 2
10625 км 2 / час 2 = 2
SQRT (10 625 км 2 / час 2 ) =
рэндов103.1 км / ч = рэнд
Направление результирующей скорости можно определить с помощью тригонометрической функции. Поскольку скорость в плоскости и скорость ветра образуют прямоугольный треугольник при сложении по схеме «голова к хвосту», угол между результирующим вектором и вектором, направленным на юг, можно определить с помощью функций синуса, косинуса или тангенса. Можно использовать касательную функцию; это показано ниже:
загар (тета) = (напротив / рядом)загар (тета) = (25/100)
тета = invtan (25/100)
тета = 14.0 градусов
Если результирующая скорость самолета составляет угол 14,0 градусов с направлением на юг (тета на диаграмме выше), то направление результирующей скорости равно 256 градусам. Как и любой вектор, результирующее направление измеряется как угол поворота против часовой стрелки с востока.
Анализ движения речного суднаВоздействие ветра на самолет аналогично действию речного течения на моторную лодку.Если бы моторная лодка плыла прямо через реку (то есть, если бы лодка была направлена носом прямо на другую сторону), она не достигла бы берега прямо напротив своей начальной точки. Речное течение влияет на движение лодки и несет ее вниз по течению. Моторная лодка может двигаться со скоростью 4 м / с прямо через реку, но результирующая скорость лодки будет больше 4 м / с и под углом в направлении вниз по течению. В то время как спидометр лодки может показывать 4 м / с, ее скорость относительно наблюдателя на берегу будет более 4 м / с.
Результирующую скорость моторной лодки можно определить так же, как это было сделано для самолета. Результирующая скорость лодки — это векторная сумма скорости лодки и скорости реки. Поскольку лодка плывет прямо через реку, а течение всегда направлено прямо вниз по течению, два вектора находятся под прямым углом друг к другу. Таким образом, теорему Пифагора можно использовать для определения результирующей скорости. Предположим, что река движется со скоростью 3 м / с на север, а моторная лодка движется со скоростью 4 м / с на восток.Какова будет результирующая скорость моторной лодки (т. Е. Скорость относительно наблюдателя на берегу)? Величину результирующего можно найти следующим образом:
(4,0 м / с) 2 + (3,0 м / с) 2 = R 216 м 2 / с 2 + 9 м 2 / с 2 = R 2
25 м 2 / с 2 = R 2
SQRT (25 м 2 / с 2 ) =
рэнд5.0 м / с =
рэндНаправление результирующего вектора — это угол поворота против часовой стрелки, который результирующий вектор делает относительно востока. Этот угол можно определить с помощью тригонометрической функции, как показано ниже.
загар (тета) = (напротив / рядом)загар (тета) = (3/4)
тета = invtan (3/4)
тета = 36,9 градуса
Учитывая скорость лодки 4 м / с, восток и скорость реки 3 м / с, север, результирующая скорость лодки будет 5 м / с при 36.9 градусов.
Подобные проблемы с моторными лодками обычно сопровождаются тремя отдельными вопросами:
- Какова результирующая скорость (как величина, так и направление) лодки?
- Если ширина реки составляет X метров, то сколько времени требуется лодке, чтобы добраться от берега до берега?
- На каком расстоянии ниже по течению лодка достигает противоположного берега?
На первый из этих трех вопросов был дан ответ выше; результирующую скорость лодки можно определить с помощью теоремы Пифагора (величина) и тригонометрической функции (направление).На второй и третий из этих вопросов можно ответить, используя уравнение средней скорости (и много логики).
пр. скорость = расстояние / время
Рассмотрим следующий пример.
| Пример 1 Моторная лодка, движущаяся со скоростью 4 м / с на востоке, встречает поток, движущийся со скоростью 3,0 м / с на севере.
|
Решение первого вопроса уже было показано в приведенном выше обсуждении.Результирующая скорость лодки составляет 5 м / с под углом 36,9 градуса. Мы начнем со второго вопроса.
Ширина реки 80 метров. То есть расстояние от берега до берега, измеренное прямо через реку, составляет 80 метров. Время, чтобы пересечь эту реку шириной 80 метров, можно определить, переставив и подставив в уравнение средней скорости.
время = расстояние / (средн. Скорость)Подставим в числитель расстояние 80 м.А как насчет знаменателя? Какое значение следует использовать для средней скорости? Следует ли использовать 3 м / с (текущая скорость), 4 м / с (скорость лодки) или 5 м / с (результирующая скорость) в качестве среднего значения скорости для преодоления 80 метров? С какой средней скоростью лодка пересекает реку шириной 80 метров? Большинство студентов хотят использовать в уравнении результирующую скорость, поскольку это фактическая скорость лодки относительно берега. Тем не менее, значение 5 м / с — это скорость, с которой лодка преодолевает диагональный размер реки.И расстояние по диагонали через реку в этом случае неизвестно. Если бы кто-то знал расстояние C на диаграмме ниже, то среднюю скорость C можно было бы использовать для расчета времени, необходимого для достижения противоположного берега. Точно так же, если кто-то знает расстояние B на диаграмме ниже, то средняя скорость B может быть использована для расчета времени достижения противоположного берега. И, наконец, если кто-то знает расстояние A на диаграмме ниже, то средняя скорость A может быть использована для расчета времени достижения противоположного берега.
В нашей задаче 80 м соответствует расстоянию A, поэтому средняя скорость 4 м / с (средняя скорость в направлении прямо через реку) должна быть подставлена в уравнение для определения времени.
время = (80 м) / (4 м / с) = 20 сДля перехода лодки через реку требуется 20 с. В течение этих 20 секунд перехода через реку лодка также плывет вниз по течению. В части c задачи задается вопрос: «На каком расстоянии ниже по течению лодка достигает противоположного берега?» То же самое уравнение необходимо использовать для расчета расстояния ниже по потоку .И снова возникает вопрос, какое из трех средних значений скорости должно использоваться в уравнении для расчета расстояния вниз по потоку? Расстояние ниже по потоку соответствует Расстояние B на диаграмме выше. Скорость, с которой лодка преодолевает это расстояние, соответствует средней скорости B на диаграмме выше (то есть скорость, с которой движется течение — 3 м / с). Таким образом, средняя скорость 3 м / с (средняя скорость в направлении вниз по потоку) должна быть подставлена в уравнение для определения расстояния.
расстояние = пр. скорость * время = (3 м / с) * (20 с)расстояние = 60 м
Лодка переносится на 60 метров вниз по течению за 20 секунд, необходимых для перехода через реку.
Математика вышеупомянутой задачи не сложнее, чем деление или умножение двух числовых величин друг на друга. Математика — это просто! Сложность проблемы носит концептуальный характер; трудность заключается в том, чтобы решить, какие числа использовать в уравнениях.Это решение вытекает из концептуального понимания (или, к сожалению, неправильного понимания) сложного происходящего движения. Движение речного судна можно разделить на две одновременные части — движение прямо через реку и движение вниз по течению. Эти две части (или компоненты) движения происходят одновременно в течение одного и того же времени (которое составляло 20 секунд в приведенной выше задаче). Решение о том, какое значение скорости или значение расстояния использовать в уравнении, должно соответствовать приведенной выше диаграмме.Двигатель лодки — это то, что переносит лодку через реку Расстояние A ; и поэтому любой расчет, включающий Расстояние A , должен включать значение скорости, обозначенное как Speed A (скорость лодки относительно воды). Точно так же это течение реки несет лодку вниз по течению Расстояние B ; и поэтому любой расчет, включающий Расстояние B , должен включать значение скорости, обозначенное как Speed B (скорость реки).Вместе эти две части (или компоненты) складываются в результирующее движение лодки. То есть поперечная составляющая смещения добавляет к смещению вниз по течению, чтобы равняться результирующему смещению. Точно так же скорость лодки (через реку) прибавляется к скорости реки (вниз по реке), чтобы равняться результирующей скорости. Таким образом, любое вычисление расстояния C или средней скорости C («Результирующая скорость») может быть выполнено с использованием теоремы Пифагора.
Теперь, чтобы проиллюстрировать важный момент, давайте попробуем второй пример задачи, который похож на первый пример задачи.Попробуйте ответить на три вопроса, а затем нажмите кнопку, чтобы проверить свой ответ.
| Пример 2 Моторная лодка, двигающаяся со скоростью 4 м / с на востоке, встречает течение 7,0 м / с на севере.
|
Важная концепция вытекает из анализа двух приведенных выше примеров проблем.В примере 1 время пересечения реки шириной 80 метров (при движении 4 м / с) составило 20 секунд. Это было при скорости течения 3 м / с. В Примере 2 скорость течения была намного больше — 7 м / с, но время для перехода через реку осталось неизменным. Фактически, сама скорость течения не влияет на время, необходимое лодке, чтобы пересечь реку. Река движется вниз по течению параллельно берегу реки. Таким образом, течение не может помочь лодке пересечь реку.Хотя повышенное течение может повлиять на результирующую скорость, заставляя лодку двигаться с большей скоростью по отношению к наблюдателю на земле, это не увеличивает скорость в направлении через реку. Компонент результирующей скорости, который увеличивается, является составляющей, направленной вниз по реке. Часто говорят, что «перпендикулярные компоненты движения не зависят друг от друга». Применительно к проблемам с речным судном это будет означать, что переменная для реки через реку не будет зависеть от (т.е., не зависит от) нижестоящей переменной. Время для перехода через реку зависит от скорости, с которой лодка пересекает реку. Только составляющая движения, направленная через реку (то есть скорость лодки), влияет на время прохождения расстояния непосредственно через реку (в данном случае 80 м). Компонент движения, перпендикулярный этому направлению — скорость течения — влияет только на расстояние, которое лодка проходит по реке. Эта концепция перпендикулярных компонентов движения будет исследована более подробно в следующей части Урока 1.
Проверьте свое понимание1. Самолет может двигаться со скоростью 80 миль / ч по отношению к воздуху. Определите результирующую скорость самолета (только величину), если он встретит
а. Встречный ветер 10 миль / ч.г. 10 миль / ч, попутный ветер.
г. 10 миль / ч, боковой ветер.
г. 60 миль / ч при боковом ветре.
2. Моторная лодка, движущаяся со скоростью 5 м / с на востоке, встречает течение 2,5 м / с на севере.
а. Какова результирующая скорость моторной лодки?г. Если ширина реки составляет 80 метров, то сколько времени требуется лодке, чтобы добраться от берега до берега?
г. На каком расстоянии ниже по течению лодка достигает противоположного берега?
3.Моторная лодка, движущаяся со скоростью 5 м / с на восток, встречает поток, движущийся со скоростью 2,5 м / с на юге.
а. Какова результирующая скорость моторной лодки?г. Если ширина реки составляет 80 метров, то сколько времени требуется лодке, чтобы добраться от берега до берега?
г. На каком расстоянии ниже по течению лодка достигает противоположного берега?
4. Моторная лодка, движущаяся со скоростью 6 м / с, на восток встречает поток, движущийся 3.8 м / с, Южный.
а. Какова результирующая скорость моторной лодки?г. Если ширина реки составляет 120 метров, то сколько времени требуется лодке, чтобы добраться от берега до берега?
г. На каком расстоянии ниже по течению лодка достигает противоположного берега?
5. Если скорость течения в вопросе № 4 была увеличена до 5 м / с, то
а.сколько времени потребуется, чтобы пересечь ту же реку шириной 120 м?г. на какое расстояние вниз по течению лодка продвинется за это время?
Скорость и скорость
Скорость и скорость
Скорость — это то, насколько быстро что-то движется.
Скорость — это скорость с направлением .
Говоря, что Собака Ариэль бежит со скоростью , 9 км / ч. (километров в час) — это скорость.
Но сказать, что он бежит 9 км / ч на запад — это скорость.
| Скорость | Скорость | |
|---|---|---|
| Имеет: | величина | звездная величина и направление |
| Пример: | 60 км / ч | 60 км / ч Север |
| Пример: | 5 м / с | 5 м / с вверх |
Представьте, что что-то движется вперед и назад очень быстро: у него высокая скорость, но низкая (или нулевая) скорость.
Скорость
Скорость измеряется как расстояние, пройденное с течением времени.
Скорость = Расстояние Время
Пример: автомобиль проезжает 50 км за час.
Его средняя скорость 50 км в час (50 км / ч)
Скорость = Расстояние Время знак равно 50 км 1 час
Мы также можем использовать эти символы:
Скорость = Δs Δt
Где Δ (« Delta ») означает «изменение», а
- s означает расстояние («s» для «пробела»)
- т означает время
Пример: вы пробегаете 360 м за 60 секунд.
Скорость = Δs Δt
= 360 м 60 секунд
= 6 м 1 секунда
Итак, ваша скорость составляет 6 метров в секунду (6 м / с).
Квартир
Скорость обычно измеряется в:
- метров в секунду (м / с или мс -1 ), или
- километров в час (км / ч или км ч -1 )
км — это 1000 м, а в часе 3600 секунд, поэтому мы можем преобразовать следующим образом (см. Метод преобразования единиц, чтобы узнать больше):
1 метр 1 с × 1 км 1000 м × 3600 с 1 ч знак равно 3600 м · км · с 1000 с · м · ч знак равно 3.6 км 1 ч
Так 1 м / с равна 3,6 км / ч
Пример: Что такое 20 м / с в км / ч?
20 м / с × 3,6 км / ч 1 м / с = 72 км / ч
Пример: Что такое 120 км / ч в м / с?
120 км / ч × 1 м / с 3,6 км / ч = 33,333 … м / с
Средняя и мгновенная скорость
В примерах до сих пор вычисляется средняя скорость : как далеко что-то перемещается за период времени.
Но скорость может меняться со временем. Автомобиль может ехать быстрее и медленнее, может даже останавливаться на светофоре.
Итак, существует также мгновенная скорость : скорость в момент во времени. Мы можем попытаться измерить его, используя очень короткий промежуток времени (чем короче, тем лучше).
Пример: Сэм использует секундомер и измеряет 1,6 секунды, когда машина проезжает между двумя столбами на расстоянии 20 м друг от друга. Что такое мгновенная скорость
?Что ж, мы не знаем точно, так как машина могла ускоряться или замедляться в течение этого времени, но мы можем оценить:
20 метров 1.6 с = 12,5 м / с = 45 км / ч
Это действительно еще средняя, но близкая к мгновенной скорости.
Постоянная скорость
Когда скорость не меняется, она постоянная .
Для постоянной скорости средняя и мгновенная скорости одинаковы.
Скорость
Скорость — это скорость с направлением .
На самом деле это вектор …
… поскольку он имеет звездную величину и направление
Поскольку направление важно, скорость использует смещение вместо расстояния:
Скорость = Расстояние Время
Скорость = Рабочий объем Время в направлении.
Пример: вы идете от дома до магазина за 100 секунд, какова ваша скорость и какова ваша скорость?
Скорость = 220 м 100 с = 2,2 м / с
Скорость = 130 кв.м 100 с Восток = 1,3 м / с Восток
Вы забыли свои деньги, поэтому поворачиваетесь и возвращаетесь домой еще через 120 секунд: какова ваша скорость и скорость туда и обратно?
Общее время 100 с + 120 с = 220 с:
Скорость = 440 м 220 с = 2.0 м / с
Скорость = 0 м 220 с = 0 м / с
Да, скорость равна нулю, когда вы закончили с того места, где начали.
Узнайте больше на Vectors.
Родственник
Движение относительно. Когда мы говорим, что что-то «покоится» или «движется со скоростью 4 м / с», мы забываем сказать «относительно меня» или «относительно земли» и т. Д.
Подумайте вот о чем: вы действительно стоите на месте? Вы находитесь на планете Земля, которая вращается со скоростью 40 075 км в день (около 1675 км / ч или 465 м / с) и движется вокруг Солнца со скоростью около 100 000 км / ч, которое само движется через Галактику.
В следующий раз, когда вы будете гулять, представьте, что вы неподвижны, и это мир движется у вас под ногами. Чувствует себя прекрасно.
Это все относительно!
Если вы едете со скоростью 100 км / ч и увеличиваете скорость до 110 км / ч, сколько времени вы выигрываете на 10 км?
Параметры не показаны, так как это один из 1000 оплачиваемых вопросов.
Купите все 1000 вопросов сейчас
Книга водительских прав (19-е издание, стр. 84):
“ Если вы увеличите среднюю скорость на 10 км / ч, выигрыш времени на 10 км составит:
— примерно 1 минута при скорости ниже 90 км / ч
— примерно ½ минуты при скорости более 90 км / ч ”
По всей вероятности, вам не понадобится знать следующие математические вычисления для реального теста.Достаточно знать, что выигрыш во времени минимален.
Метод 1
| Цветовые коды фигур (их легче отслеживать) | |
| Исходная скорость | 100 км / ч |
| Новая скорость | 110 км / ч |
| Минут в час (так как скорость км / ч, километров в час ) | 60 минут |
| Километров | 10 км |
Сначала подсчитаем, сколько минут нужно, чтобы проехать 1 км на обеих скоростях:
- 60/100 = требуется 0.6 минут на дорогу 1 км
- 60/110 = 1 км занимает 0,54 минуты
Следовательно, на более высокой скорости требуется немного меньше времени. Разница:
- 0,6 — 0,54 = 0,06 минуты на 1 км быстрее при движении со скоростью 110 км / ч по сравнению со 100 км / ч.
Однако вопрос в том, сколько времени вы выигрываете на 10 км , а не на км. Поэтому пересчитаем выигрыш по времени на 10 км:
- 0,06 * 10 = 0.6 минут выигрыша по времени на 10 км
Теперь это действительно сделано. Однако легче понять, если ответ пересчитан в секунды:
Метод 2
| Цветовые коды фигур (их легче отслеживать) | |
| Исходная скорость | 100 км / ч |
| Новая скорость | 110 км / ч |
| Расстояние | 10 км = 10000 метров |
| Фиксированная скорость пересчета км / ч в м / с | 3.6 раз |
Формула для расчета времени:
Для работы формулы требуется, чтобы мы использовали метры вместо 10 км и метры в секунду (м / с) вместо километров в час (км / ч). Поэтому скорости пересчитываются в м / с:
- 100 / 3,6 = 27,78 м / с
- 110 / 3,6 = 30,56 м / с
Только теперь мы можем использовать формулу Расстояние / скорость = время :
- 10,000 / 27,78 = 360 с
- 10,000 / 30.56 = 327 с
Затем мы можем вычислить разницу во времени между обеими скоростями:
Это пример одного из вопросов по теории вождения на Körtkortonline.se (также в теоретических тестах на арабском языке).
В Интернете также есть книжка с водительскими правами (2021 г.).
Еще примеры вопросов по теории:
q6-a-автомобиль-путешествует-со-скоростью-30 | LIDO
Решение:
Скорость автомобиля за первые 30 минут = 30 км ч ^ {- 1}
Скорость автомобиля на следующий 1 час = 40 км ч ^ {- 1}
(а) общее расстояние, пройденное автомобилем
Первый корпус
Скорость = расстояние / время
расстояние = скорость x время
= 30 х 0.{-1}
«привет, добро пожаловать в начало сегодня едем на машине со скоростью 30 километров в час за 30 минут и со скоростью 40 километр в час для один час, давайте узнаем общую сумму сначала расстояние, а затем путешествие во времени и средняя скорость машина так давайте выясним общее расстояние так сначала нам нужно узнать расстояние до каждая вещь так что первым делом 30 километров расстояние равно скорости во времени скорость равна 30 км и в время равно один за другим, так что будет 15 итак 15 грамм путешествия и второй расстояние равно скорости во времени значит скорость равна 40, а затем время равно 1 часу и это будет 40 километров хорошо, какое общее расстояние вы можете возьми это здесь общее расстояние идет быть 15 плюс 40 итак 65 километров он проехал итого общее пройденное расстояние составляет 65 километров Итак, давайте узнаем общее время, чтобы мы могу сделать это очень легко общее время — общее время будет Найдите время здесь, так что один час игры 1.0,5 часа это будет сколько 1,5 часа хорошо, это общее время, а затем просят среднюю скорость так давайте узнаем среднюю скорость так это наша скорость формула нашей скорости вы знаете всего расстояние по общему затраченному времени так что давайте теперь сделаем среднюю скорость я не знаю давайте сделаем общую среднюю скорость расстояние по общему затраченному времени общее расстояние по общему затраченному времени общее расстояние равно 65 и всего затраченное время равно 1,5 часа поэтому пройденное расстояние будет 55 км 40 плюс вы можете извиниться, это всего 55 40 плюс 55 хорошо, да, это 40 плюс 15 так что вы можете принять это как 55 55 ноты на musicaneo5 это означает, что что значит 30 6,67 км на час окей, это будет 36 км в час да, я сделал ошибку здесь мы можем видеть это только 40 плюс 50 равно 55 хорошо, мы степень 65 итого общее время составляет 55 километров, а общее расстояние 55, а общее время 1.5, так что это будет средняя скорость в среднем скорость, надеюсь, вы поняли видео подписывайтесь на канал для регулярных обновления и спасибо за просмотр этого видео «
.

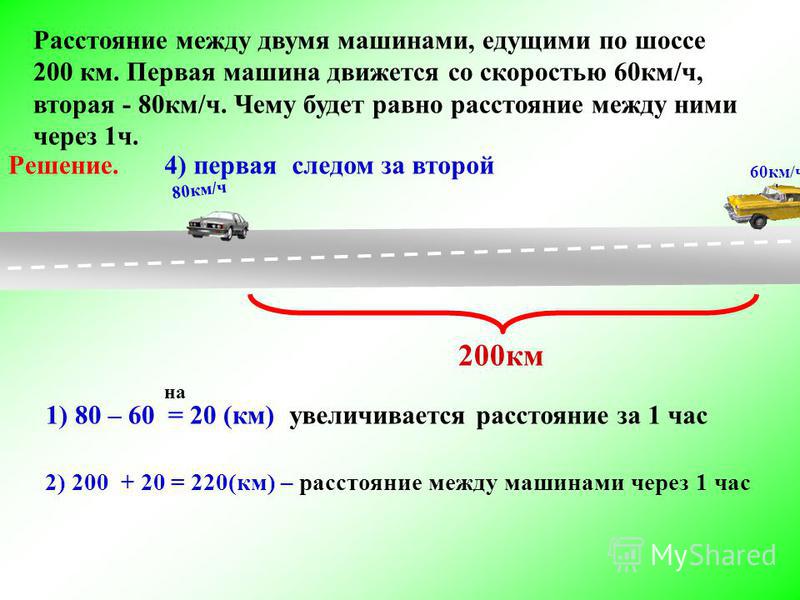
 Усвоил?
Усвоил? Ответ дайте в км/ч.
Ответ дайте в км/ч.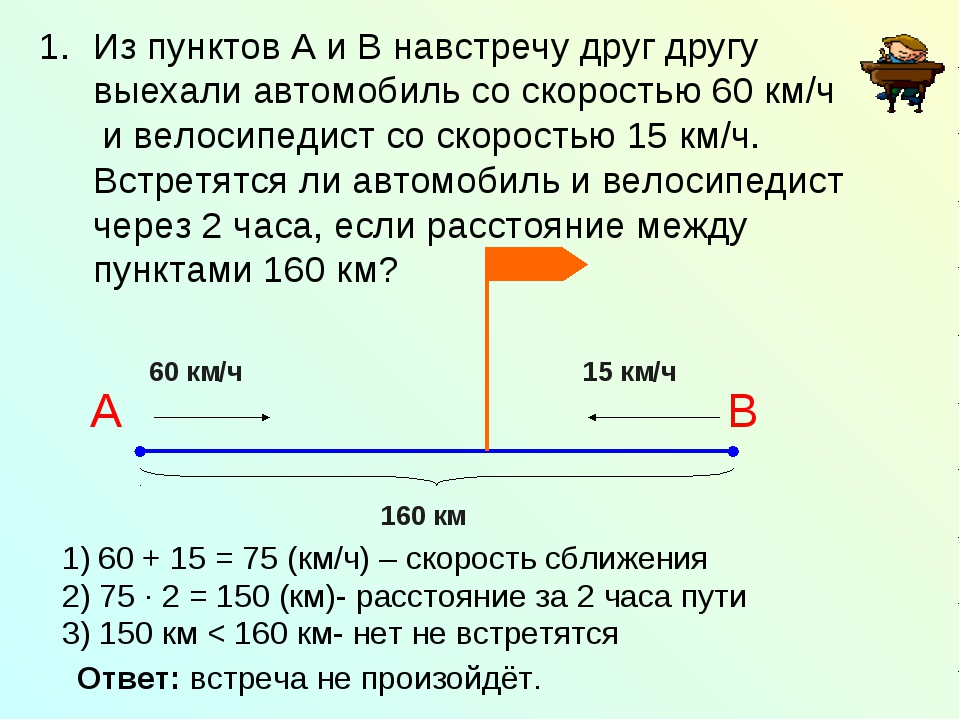
 Найдите частное.
Найдите частное.